2022-2023学年江苏省泰州市海陵区八年级(下)期中数学试卷
发布:2024/7/11 8:0:9
一、选择题(每题3分,共18分)
-
1.下列数学符号属于中心对称图形的是( )
组卷:192引用:7难度:0.9 -
2.某市今年共有6万名考生参加中考,为了了解这6万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析,以下说法正确的有( )
①这种调查采用了抽样调查的方式;
②6万名考生是总体;
③所抽取的1000名考生的数学成绩是总体的一个样本;
④样本容量是1000名考生.组卷:65引用:2难度:0.7 -
3.将一个正六面体骰子掷一次,它的点数恰好是4的概率是( )
组卷:86引用:3难度:0.9 -
4.分式
中,当x=m时,下列说法正确的是( )x-mx-1组卷:201引用:2难度:0.9 -
5.用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中( )
组卷:1728引用:11难度:0.7 -
6.菱形ABCD的周长为32cm,则菱形ABCD的面积的最大值为( )
组卷:400引用:4难度:0.5
二、填空题(每题3分,共30分)
-
7.“买一张彩票,中一等奖”是
(填“必然”、“不可能”或“随机”)事件.组卷:208引用:6难度:0.7 -
8.已知一个样本中,样本容量为50,这50个数据分别落在5个小组内,第一、二、四、五小组的频数依次是2,10,10,20,那么第三个小组的频率是.
组卷:267引用:5难度:0.9
三、解答题(本题共10题,共102分)
-
25.【问题情境】如图1,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE′.延长AE交CE′于点F,连接DE.
【猜想证明】
(1)试判断四边形BE′FE的形状,并说明理由;
(2)如图2,若DA=DE,猜想线段CF与FE′的数量关系并加以证明;
【解决问题】
(3)如图1若BE=3,CF=1,求DE.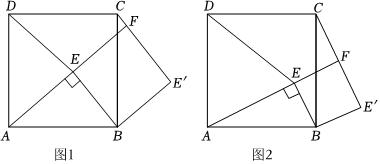 组卷:311引用:3难度:0.3
组卷:311引用:3难度:0.3 -
26.如图1,在平面直角坐标系中,点A的坐标是(0,8),点B的坐标是(6,0),点C为AB的中点,动点P从点A出发,沿AO方向以每秒1个单位的速度向终点O运动,同时动点Q从点O出发,以每秒2个单位的速度沿射线OB方向运动;当点P到达点O时,点Q也停止运动.以CP,CQ为邻边构造▱CPDQ,设点P运动的时间为t秒.
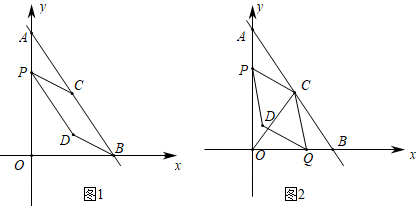
(1)点C的坐标为,直线AB的解析式为.
(2)当点Q运动至点B时,连接CD,求证:CD∥AP.
(3)如图2,连接OC,当点D恰好落在△OBC的边所在的直线上时,求所有满足要求的t的值.组卷:1565引用:8难度:0.2


