2023年广东省深圳市宝安区桃源中澳中学中考数学三模试卷

一.选择题（共10小题，满分30分，每小题3分）

• 1．cos60°的值等于（　　）

  A． 1 2

  B． 2 2

  C． 3 2

  D．1
  组卷：386引用：5难度：0.9

  解析

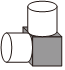• 2．我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法．“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体．如图所示的几何体是可以形成“牟合方盖”的一种模型，它的俯视图是（　　）

  A．

  B．

  C．

  D．
  组卷：895引用：40难度：0.8

  解析

• 3．下列计算错误的是（　　）

  A．a•a=a2

  B．2a+a=3a

  C．（a3）2=a5

  D．a3÷a-1=a4
  组卷：996引用：55难度：0.9

  解析

• 4．在一个不透明的布袋中装有50个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在0.3左右，则布袋中白球可能有（　　）

  A．15个

  B．20个

  C．30个

  D．35个
  组卷：2657引用：45难度：0.9

  解析

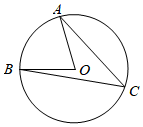• 5．如图，点A、B、C是⊙O上的三个点，若∠AOB=76°，则∠C的度数为（　　）

  A．76°

  B．38°

  C．24°

  D．33°
  组卷：1071引用：10难度：0.6

  解析

• 6．把二次函数y=x²+2x+1先向右平移2个单位长度，再向上平移1个单位长度，新二次函数表达式变为（　　）

  A．y=（x+3）2+2

  B．y=（x-1）2+2

  C．y=（x-1）2+1

  D．y=（x+3）2-1
  组卷：872引用：5难度：0.5

  解析

• 7．如图，在菱形ABCD中，对角线AC，BD相交于点O，添加下列条件，能使菱形ABCD成为正方形的是（　　）

  A．AC=BD

  B．AC⊥BD

  C．AD=AB

  D．AC平分∠DAB
  组卷：1364引用：15难度：0.7

  解析

三.解答题（共7小题，满分55分）

• 21．在平面直角坐标系中，若两点的横坐标不相等，纵坐标互为相反数，则称这两点关于x轴斜对称．其中一点叫做另一点关于x轴的斜对称点．如：点（-4，2），（1，-2）关于x轴斜对称．在平面直角坐标系xOy中，点A的坐标为（2，1）．
  （1）下列各点中，与点A关于x轴斜对称的是

  （只填序号）；
  ①（3，-1），②（-2，1），③（2，-1），④（-1，-1）．
  （2）若点A关于x轴的斜对称点B恰好落在直线y=kx+1上，△AOB的面积为3，求k的值；
  
  （3）抛物线y=x²-bx-1上恰有两个点M、N与点A关于x轴斜对称，抛物线的顶点为D，且△DMN为等腰直角三角形，则b的值为

  ．
  组卷：703引用：4难度：0.5

  解析

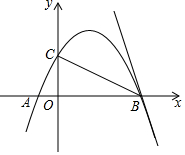• 22．如图，抛物线y=ax²+bx+2经过点A（-1，0），B（4，0），交y轴于点C；
  （1）求抛物线的解析式（用一般式表示）；
  （2）点D为y轴右侧抛物线上一点，是否存在点D使S_△ABC=

  2

  3

  S_△ABD？若存在请直接给出点D坐标；若不存在请说明理由；
  （3）将直线BC绕点B顺时针旋转45°，与抛物线交于另一点E，求BE的长．
  组卷：8232引用：12难度：0.3

  解析