2022-2023学年山东省东营市经开区八年级(下)期末数学试卷(五四学制)
发布:2024/7/12 8:0:9
一、选择题(共10小题,每题3分,共30分)
-
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
组卷:702引用:11难度:0.9 -
2.九年级一班有七个学习小组,每组人数如下:5,5,6,x,6,7,8,已知平均每个小组有6个,则这组数据的众数与中位数分别是( )
组卷:55引用:4难度:0.9 -
3.抛物线y=3(x-1)2+2的顶点坐标为( )
组卷:1595引用:16难度:0.8 -
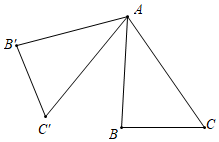 4.如图,△ABC中,∠BAC=36°,将△ABC绕点A按顺时针方向旋转70°,得到△AB′C′,则∠BAC′的度数为( )组卷:596引用:10难度:0.5
4.如图,△ABC中,∠BAC=36°,将△ABC绕点A按顺时针方向旋转70°,得到△AB′C′,则∠BAC′的度数为( )组卷:596引用:10难度:0.5 -
5.某商品原价200元,经连续两次降价后售价为162元,设平均每次降价的百分率为x,则下面所列方程正确的是( )
组卷:379引用:11难度:0.6 -
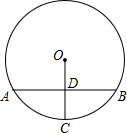 6.如图,⊙O的弦AB垂直平分半径OC,垂足为D,若CD=,则AB的长为( )22组卷:892引用:7难度:0.9
6.如图,⊙O的弦AB垂直平分半径OC,垂足为D,若CD=,则AB的长为( )22组卷:892引用:7难度:0.9 -
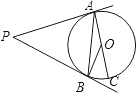 7.如图,PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为( )组卷:2396引用:35难度:0.9
7.如图,PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为( )组卷:2396引用:35难度:0.9 -
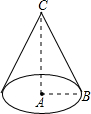 8.如图,已知在Rt△ABC中,∠BAC=90°,AB=3,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )组卷:234引用:41难度:0.9
8.如图,已知在Rt△ABC中,∠BAC=90°,AB=3,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )组卷:234引用:41难度:0.9
三、解答题(共62分)
-
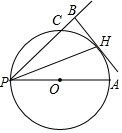 24.如图,在⊙O中,PA是直径,PC是弦,PH平分∠APB且与⊙O交于点H,过H作HB⊥PC交PC的延长线于点B.
24.如图,在⊙O中,PA是直径,PC是弦,PH平分∠APB且与⊙O交于点H,过H作HB⊥PC交PC的延长线于点B.
(1)求证:HB是⊙O的切线;
(2)若HB=4,BC=2,求⊙O的直径.组卷:1906引用:8难度:0.5 -
25.如图1,抛物线y=-x2+bx+c与x轴交于A(2,0),B(-4,0)两点.
(1)求该抛物线的解析式;
(2)若抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在抛物线的第二象限图象上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若不存在,请说明理由.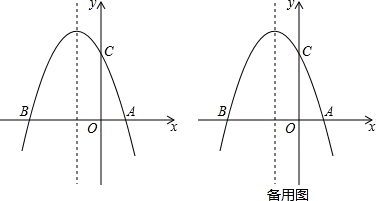 组卷:2365引用:19难度:0.5
组卷:2365引用:19难度:0.5


