2022-2023学年广东省广州市黄埔区八年级（下）期末数学试卷

一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．下列二次根式中，最简二次根式是（　　）

  A． 7

  B． 9

  C． 12

  D． 2 3
  组卷：463引用：13难度：0.8

  解析

• 2．一次函数的图象y=x-5不经过第（　　）象限．

  A．一

  B．二

  C．三

  D．四
  组卷：181引用：1难度：0.5

  解析

• 3．下列各式中，正确的是（　　）

  A． （ - 10 ） 2 = - 10

  B． （ ± 10 ） 2 =± 10

  C． 10 2 =± 10

  D． 10 2 = 10
  组卷：196引用：1难度：0.7

  解析

• 4．以下列各组数为边长，能构成直角三角形的是（　　）

  A．5，12，14

  B．7，24，26

  C．6，8，10

  D．1，1， 3
  组卷：115引用：1难度：0.7

  解析

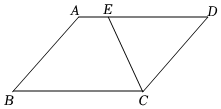• 5．如图，在平行四边形ABCD中，∠A=130°，CE平分∠BCD，则∠DCE度数是（　　）

  A．50°

  B．60°

  C．62°

  D．65°
  组卷：171引用：1难度：0.7

  解析

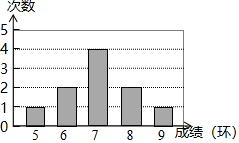• 6．一名射击运动员连续打靶10次，命中的环数如图所示，这位运动员命中环数的众数与中位数分别为（　　）

  A．7与7

  B．7与7.5

  C．8与7.5

  D．8与7
  组卷：244引用：3难度：0.6

  解析

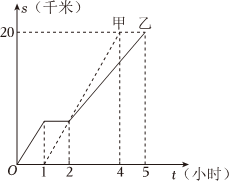• 7．甲、乙两同学从A地出发，沿同一条路到B地，乙先出发，他们离出发地的距离s（千米）与行驶时间t（小时）之间的函数关系图象如图所示，下列说法中不符合图象描述的是（　　）

  A．他们都行驶了20千米

  B．乙在途中停留了1小时

  C．甲、乙两人同时到达目的地

  D．乙出发2小时后，两人相遇
  组卷：325引用：3难度：0.7

  解析

• 8．下列四个命题中不正确的是（　　）

  A．对角线相等的平行四边形是矩形

  B．对角线互相垂直的四边形是菱形

  C．对角线相等的菱形是正方形

  D．对角线互相平分的四边形是平行四边形
  组卷：598引用：13难度：0.8

  解析

三、解答题（本大题共9小题，满分72分，解答应写出文字说明、证明过程或演算步骤．）

• 24．如图，四边形OABC是矩形，点A，C别在x轴，y轴上，点B的坐标是（4，3），∠OBA的平分线与x轴交于点E．
  （1）求线段OB的长；
  （2）求直线BE的解析式；
  （3）连接CA，交BE于点F，连接OF，点N是平面内任意一点，在x轴上是否存在点M，使得以O，F，M，N为顶点且以OF为边的四边形为菱形？若存在，请求出点M的坐标；若不存在，请说明理由．
  
  组卷：1235引用：2难度：0.4

  解析

• 25．如图，四边形ABCD是正方形，AB=40，点G是射线BC上的动点（不与点B，C重合），DE⊥AG于点E，BF⊥AG于点F．
  
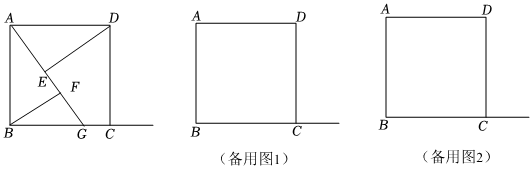
  （1）当点G在线段BC上时，求证：AE=BF；
  （2）若BG=30，求BF+EF的长；
  （3）点G在射线BC上运动过程中，连接DF，CE，判断线段DF与CE的数量关系及直线DF与CE的位置关系，并说明理由．
  组卷：654引用：4难度：0.3

  解析