2023年甘肃省平凉四中中考数学三模试卷

一、选择题（本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．-4的相反数是（　　）

  A． 1 4

  B．4

  C．-4

  D．±4
  组卷：201引用：10难度：0.9

  解析

• 2．下列既是中心对称图形又是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：20引用：1难度：0.5

  解析

• 3．近年来出生人口持续走低，即使国家开放三胎，也缓解不了颓势，2022年我国出生人口是1062万人，数据1062万用科学记数法表示应为（　　）

  A．1062×104

  B．10.62×106

  C．1.062×107

  D．0.1062×108
  组卷：84引用：7难度：0.8

  解析

• 4．关于x的一元二次方程x²+4x+k=0有两个实数根，则k的取值范围是（　　）

  A．k≤-4

  B．k＜-4

  C．k≤4

  D．k＜4
  组卷：1671引用：36难度：0.7

  解析

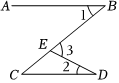• 5．如图，AB∥CD，点E在BC上，若∠1=40°，∠2=20°，则∠3的度数是（　　）

  A．60°

  B．70°

  C．80°

  D．50°
  组卷：43引用：3难度：0.7

  解析

• 6．直线y=kx+b经过一、三、四象限，那么点（b,k）第（　　）象限．

  A．四

  B．三

  C．二

  D．一
  组卷：589引用：6难度：0.6

  解析

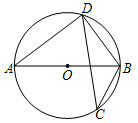• 7．如图，已知AB是⊙O的直径，CD是弦，若∠BCD=36°，则∠ABD等于（　　）

  A．54°

  B．56°

  C．64°

  D．66°
  组卷：2170引用：28难度：0.7

  解析

• 8．我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽．每株脚钱三文足，无钱准与一株椽．”其大意为：现请人代买一批椽，这批椽的价钱为6210文．如果每株椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？设这批椽的数量为x株，则符合题意的方程是（　　）

  A．3（x-1）= 6210 x	B． 6210 x - 1 =3
  C．3x-1= 6210 x	D． 6210 x =3
  组卷：4334引用：98难度：0.9

  解析

• 9．道路施工部门在铺设如图所示的管道时，需要先按照其中心线计算长度后再备料．图中的管道中心线

  ˆ

  AB

  的长为（单位：m）（　　）

  A． 40 π 3

  B． 80 π 3

  C． 1600 π 3

  D． 3200 π 3
  组卷：517引用：8难度：0.7

  解析

四、解答题（二）：（本大题共5小题，共50分.解答时，应写出必要的文字说明、证明过程或演算步骤）

• 27．问题情境：数学活动课上，老师组织同学们以“正方形”为主题开展数学活动．
  动手实践：
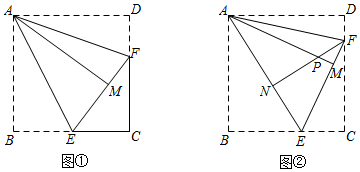
  （1）如图①，已知正方形纸片ABCD，勤奋小组将正方形纸片沿过点A的直线折叠，使点B落在正方形ABCD的内部，点B的对应点为点M，折痕为AE，再将纸片沿过点A的直线折叠，使AD与AM重合，折痕为AF，易知点E、M、F共线，则∠EAF=

  度．
  拓展应用：
  （2）如图②，腾飞小组在图①的基础上进行如下操作：将正方形纸片沿EF继续折叠，使得点C的对应点为点N，他们发现，当点E的位置不同时，点N的位置也不同，当点E在BC边的某一位置时，点N恰好落在折痕AE上．
  ①则∠CFE=

  度．
  ②设AM与NF的交点为点P，运用（1）、（2）操作所得结论，求证：△ANP≌△FNE．
  解决问题：
  （3）在图②中，若AB=3，请直接写出线段MP的长．
  组卷：1092引用：9难度：0.3

  解析

• 28．如图，在平面直角坐标系中，抛物线y=-

  1

  3

  x²+bx+c与x轴交于A（-1，0）、B（3，0）两点，与y轴交于点C，点D是点C关于x轴的对称点．
  （1）求抛物线与直线BD的解析式；
  （2）点P为直线BC上方抛物线上一动点，当△BPC的面积最大时，求点P的坐标；
  （3）在（2）的条件下，当△BPC的面积最大时，在抛物线的对称轴上有一动点M，在BD上有一动点N，且MN⊥BD，求PM+MN的最小值．
  
  组卷：66引用：1难度：0.3

  解析