2020-2021学年广东省广州市番禺区桥城中学九年级（上）期中数学试卷

一、选择题（共十题：共30分）

• 1．如图是我国几家银行的标志，其中既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：343引用：14难度：0.9

  解析

• 2．已知x=1是关于x的一元二次方程（m-1）x²+x+1=0的一个根，则m的值是（　　）

  A．1

  B．-1

  C．0

  D．无法确定
  组卷：1218引用：77难度：0.9

  解析

• 3．在平面直角坐标系中，点A（-2，-1）绕原点O逆时针旋转180°得到点B，则点B的坐标是（　　）

  A．（-1，-2）

  B．（-2，1）

  C．（2，-1）

  D．（2，1）
  组卷：83引用：5难度：0.9

  解析

• 4．方程x²=x的解是（　　）

  A．x=1

  B．x=0

  C．x1=1，x2=0

  D．x1=0，x2=-1
  组卷：145引用：6难度：0.7

  解析

• 5．把函数y=x²的图象向右平移1个单位，所得函数表达式为（　　）

  A．y=x2+1

  B．y=（x+1）2

  C．y=x2-1

  D．y=（x-1）2
  组卷：305引用：10难度：0.8

  解析

• 6．关于x的一元二次方程kx²+2x-1=0有两个不相等实数根，则k的取值范围是（　　）

  A．k＞-1

  B．k≥-1

  C．k≠0

  D．k＞-1且k≠0
  组卷：2064引用：37难度：0.7

  解析

• 7．设A（-2，y₁），B（1，y₂），C（2，y₃）是抛物线y=-（x+1）²+m上的三点，则y₁，y₂，y₃的大小关系是
  （　　）

  A．y1＞y2＞y3

  B．y1＞y3＞y2

  C．y3＞y2＞y1

  D．y2＞y1＞y3
  组卷：320引用：10难度：0.7

  解析

• 8．在元旦庆祝活动中，参加活动的同学互赠贺卡，共送贺卡90张，则参加活动的有（　　）人．

  A．9

  B．10

  C．12

  D．15
  组卷：1632引用：6难度：0.5

  解析

三、解答题（共九题：共66分）

• 24．使得函数值为零的自变量的值称为函数的零点．例如，对于函数y=x-1，令y=0，可得x=1，我们就说1是函数y=x-1的零点，已知函数y=x²-2mx-2（m+3）（m为常数）．
  （1）当m=0时，求该函数的零点；
  （2）证明：无论m取何值，该函数总有两个零点；
  （3）设函数的两个零点分别为x₁和x₂，且

  1

  x

  1

  +

  1

  x

  2

  =

  -

  1

  4

  ，此时函数图象与x轴的交点分别为A、B（点A在点B左侧），求点A与点B的距离．
  组卷：20引用：2难度：0.5

  解析

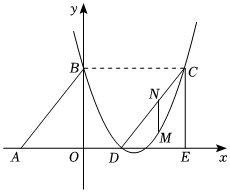• 25．如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（-3，0）、（0，4），抛物线y=

  2

  3

  x²+bx+c经过B点，且顶点在直线x=

  5

  2

  上．
  （1）求抛物线对应的函数关系式；
  （2）若△DCE是由△ABO沿x轴向右平移得到的，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由．
  （3）在（2）的条件下，若M点是CD所在直线下方该抛物线上的一个动点，过点M作MN平行于y轴交CD于点N．设点M的横坐标为t,MN的长度为s,求s与t之间的函数关系式，写出自变量t的取值范围，并求s取大值时，点M的坐标．
  组卷：1790引用：9难度：0.1

  解析