人教版（2019）必修第二册《7.3 万有引力理论的成就》2024年同步练习卷（25）

一、选择题

• 1．地球半径为R，地球表面的重力加速度为g,若高空中某处的重力加速度为

  g

  4

  ，则该处距地球表面的高度为（　　）

  A．R

  B．2R

  C． 2 R

  D．3R
  组卷：87引用：10难度：0.7

  解析

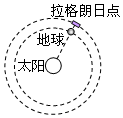• 2．2011年8月“嫦娥二号”成功进入了环绕“日地拉格朗日点”的轨道，我国成为世界上第三个造访该点的国家。如图，该拉格朗日点位于太阳和地球连线的延长线上，一飞行器处于该点，在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动，则此飞行器的（　　）

  A．线速度小于地球的线速度

  B．向心加速度大于地球的向心加速度

  C．向心力仅由太阳的引力提供

  D．向心力仅由地球的引力提供
  组卷：279引用：14难度：0.9

  解析

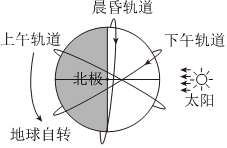• 3．2021年7月我国成功将全球首颗民用晨昏轨道气象卫星一“风云三号05星”送入预定圆轨道，轨道周期约为1.7h,被命名为“黎明星”，使我国成为国际上唯一同时拥有晨昏、上午、下午三条轨道气象卫星组网观测能力的国家，如图所示某时刻“黎明星”正好经过赤道上P城市正上方，已知地球表面的重力加速度g取9.8m/s²，则下列说法正确的是（　　）

  A．“黎明星”做匀速圆周运动的向心加速度大于9.8m/s2

  B．“黎明星”做匀速圆周运动的线速度大于7.9km/s

  C．该时刻后“黎明星”经过1.7h能经过P城市正上方

  D．该时刻后“黎明星”经过17天能经过P城市正上方
  组卷：39引用：1难度：0.4

  解析

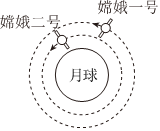• 4．2010年10月1日“嫦娥二号”成功发射。其环月飞行的高度为100km,所探测到的有关月球的数据将比环月飞行高度为200km的“嫦娥一号”更加翔实。若两颗卫星环月的运行均可视为匀速圆周运动，运行轨道如图所示。则（　　）

  A．“嫦娥二号”环月运行的周期比“嫦娥一号”小

  B．“嫦娥二号”环月运行的线速度比“嫦娥一号”小

  C．“嫦娥二号”环月运行的向心加速度比“嫦娥一号”小

  D．“嫦娥二号”环月运行的向心力与“嫦娥一号”相等
  组卷：336引用：3难度：0.8

  解析

• 5．经长期观测人们在宇宙中已经发现了“双星系统”。“双星系统”由两颗相距较近的恒星组成，每个恒星的线度远小于两个星体之间的距离，而且双星系统一般远离其他天体。如图所示，两颗星球组成的双星，在相互之间的万有引力作用下，绕连线上的O点做周期相同的匀速圆周运动。现测得两颗星之间的距离为L，质量之比为m₁：m₂=3：2。则可知（　　）

  A．m1做圆周运动的半径为 1 3 L

  B．m2做圆周运动的半径为 3 5 L

  C．m1、m2做圆周运动的角速度之比为2：3

  D．m1、m2做圆周运动的线速度之比为3：2
  组卷：540引用：3难度：0.5

  解析

• 6．黑洞是一种密度极大、体积极小的天体，引力大到光都无法逃脱其“魔掌”，所以黑洞无法直接被观测，但可以通过观测绕其运动的恒星，大致推测出黑洞的质量。观察发现，某恒星绕银河系中心黑洞人马座A*的周期为n年，此恒星到人马座A*的平均距离为mA.U.（地球到太阳的平均距离为1A.U.），不考虑相对论效应，则人马座A*的质量与太阳质量的比值为（　　）

  A． m 3 n 2

  B． m 2 n 3

  C． n 3 m 2

  D． n 2 m 3
  组卷：164引用：4难度：0.6

  解析

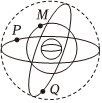• 7．如图所示是北斗导航系统中部分卫星的轨道示意图，已知P、Q、M三颗卫星均做匀速圆周运动，其中P是地球同步卫星，则（　　）

  A．卫星Q、M的加速度aQ＞aM

  B．卫星P、M的角速度ωP＜ωM

  C．卫星Q相对地面静止

  D．卫星P、Q的机械能一定相等
  组卷：17引用：1难度：0.4

  解析

二、计算题

• 8．把地球上的一个秒摆（周期等于2s的摆称为秒摆）拿到月球上去，它的振动周期变为多少？已知地球质量M_地=5.98×10²⁴kg,半径R_地=6.4×10⁶m,月球质量M_月=7.34×10²²kg,半径R_月=1.74×10⁶m.
  组卷：19引用：4难度：0.5

  解析

• 9．2021年5月15日7时18分，“天问一号”探测器成功着陆于火是乌托邦平原南部预选着陆区，我国首次火星探测任务着陆火星取得成功，探测器到达火星轨道后，并非直接登陆火星，而是多次环绕火星飞行，获得更加详细的火星温度、大气成分、气象资源等信息，传回地球来计算并确定最佳登陆地点和时间，测得“天问一号”绕火星n圈的时间为t,火星的半径为R，火星表面的重力加速度大小为g,引力常量为G，忽略火星的自转，求：
  （1）火星的质量M；
  （2）火星的第一宇宙速度v；
  （3）探测器离火星表面的高度H。
  组卷：12引用：1难度：0.4

  解析

三、解答题

• 10．相传，在1865年就读于剑桥大学的牛顿回到乡下躲避鼠疫期间，被树上掉下来的苹果砸中，由此引发他对万有引力的思考，并将地球对物体的引力与行星绕太阳运行的引力统一起来，提出了提出了万有引力定律，为经典力学体系的建立打下了坚实的基础。
  （1）由于物体随地球自转需要向心力，所以我们感受的到的重力，并不是地球对物体的吸引力。设想地球是质量为M、半径为R的均匀球体，其自转周期为T，并已知引力常量为G。请根据牛顿运动定律和万有引力定律，写出静止在地球赤道上质量为m₀的物体所受重力大小的表达式（用题中已知量的字母及相关的常量表示）；
  （2）将行星绕太阳的运动简化成匀速圆周运动，应用牛顿运动定律和开普勒第三定律（

  r

  3

  T

  2

  =k,其中r为行星中心到太阳中心间的距离，T为行星运动的周期，k为常数）等，推导行星和太阳之间的引力满足F=

  GM

  m

  r

  2

  ，其中m为行星的质量，M为太阳的质量，G是比例常数；
  （3）上面（2）的推导是源于开普勒行星运动定律。因此它只适用于行星与太阳之间的力，牛顿在此基础上又向前走了一大步，提出了任何两个质点之间都存在引力，且都满足上述（2）中的表达式。在牛顿时代已经能比较精确地测定；月球轨道半径r、月球公转周期T、地球半径R，地球表面的重力加速度g。若维持月球绕地球运动的力与使得苹果下落的力真是同一种力，求出上述4个量应满足的关系。
  组卷：109引用：1难度：0.3

  解析