2020-2021学年河南省安阳市五校联考九年级（上）期中数学试卷

一、选择题（共10小题）

• 1．下列防控疫情的图标中，既是轴对称图形，又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：537引用：30难度：0.8

  解析

• 2．若关于x的一元二次方程（a+1）x²+x+a²-1=0的一个根是0，则a的值为（　　）

  A．1

  B．-1

  C．1或-1

  D． 1 2
  组卷：1319引用：27难度：0.9

  解析

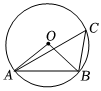• 3．如图，AB是⊙O的弦，点C在圆上，已知∠AOB=100°，则∠C=（　　）

  A．40°

  B．50°

  C．60°

  D．80°
  组卷：94引用：4难度：0.7

  解析

• 4．定义运算：m☆n=mn²-mn-1．例如：4☆2=4×2²-4×2-1=7，则方程1☆x=0的根的情况为（　　）

  A．有两个不相等的实数根	B．有两个相等的实数根
  C．无实数根	D．只有一个实数根
  组卷：3022引用：62难度：0.8

  解析

• 5．国家统计局统计数据显示，我国快递业务收入逐年增加．2017年至2019年我国快递业务收入由5000亿元增加到7500亿元．设我国2017年至2019年快递业务收入的年平均增长率为x,则可列方程为（　　）

  A．5000（1+2x）=7500

  B．5000×2（1+x）=7500

  C．5000（1+x）2=7500

  D．5000+5000（1+x）+5000（1+x）2=7500
  组卷：3861引用：67难度：0.6

  解析

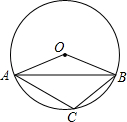• 6．如图，A、B、C在⊙O上，∠OAB=22.5°，则∠ACB的度数是（　　）

  A．11.5°

  B．112.5°

  C．122.5°

  D．135°
  组卷：753引用：13难度：0.9

  解析

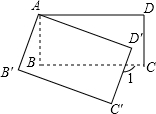• 7．如图所示，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°）．若∠1=110°，则α=（　　）

  A．20°

  B．30°

  C．40°

  D．50°
  组卷：462引用：13难度：0.9

  解析

三、解答题（共8小题）

• 22．如图1，在Rt△ABC中，∠A=90°，AB=AC，点D，E分别在边AB、AC上，AD=AE，连接DC，点M，P，N分别为DE，DC，BC的中点．
  
  （1）观察猜想：图1中，线段PM与PN的数量关系是

  ，位置关系是

  ；
  （2）探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；
  （3）拓展延伸：把△ADE绕点A在平面内自由旋转，若AD=4，AB=10．请直接写出△PMN面积的最大值．
  组卷：392引用：9难度：0.5

  解析

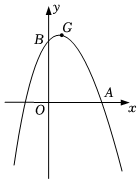• 23．如图，抛物线y=-x²+2x+c与x轴正半轴，y轴正半轴分别交于点A，B，且OA=OB，点G为抛物线的顶点．
  （1）求抛物线的解析式及点G的坐标；
  （2）点M，N为抛物线上两点（点M在点N的左侧），且到对称轴的距离分别为3个单位长度和5个单位长度，点Q为抛物线上点M，N之间（含点M，N）的一个动点，求点Q的纵坐标y_Q的取值范围；
  （3）点E是直线AB上方抛物线上的一动点，当△ABE的面积最大时，请直接写出点E的坐标和△ABE面积的最大值．
  组卷：220引用：2难度：0.5

  解析