2023年广东省广州市花都区中考数学二模试卷
发布:2024/6/20 8:0:9
一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
-
1.我国杨秉烈先生在上世纪八十年代发明了繁花曲线规画图工具,利用该工具可以画出许多漂亮的繁花曲线,繁花曲线的图案在服装、餐具等领域都有广泛运用.下面四种繁花曲线中,是轴对称图形的是( )
组卷:299引用:12难度:0.7 -
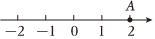 2.点A在数轴上的位置如图所示,则点A所表示的数的相反数是( )组卷:130引用:2难度:0.7
2.点A在数轴上的位置如图所示,则点A所表示的数的相反数是( )组卷:130引用:2难度:0.7 -
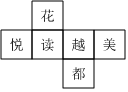 3.如图所示是一个正方体的展开图,把展开图折叠成小正方体,与“读”字相对面的字是( )组卷:84引用:3难度:0.7
3.如图所示是一个正方体的展开图,把展开图折叠成小正方体,与“读”字相对面的字是( )组卷:84引用:3难度:0.7 -
4.下列运算中,正确的是( )
组卷:460引用:7难度:0.7 -
5.不透明的盒子放有三张大小、形状及质地相同的卡片,卡片上分别写有李白《峨眉山月歌》,李白《渡荆门送别》和王维《寄荆州张丞相》三首诗,小明从盒子中随机抽取两张卡片,卡片上诗的作者都是李白的概率是( )
组卷:510引用:9难度:0.5 -
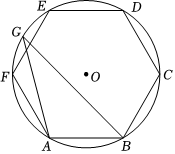 6.如图,正六边形ABCDEF内接于⊙O,点G是EF弧上的一点,则∠BGA的度数为( )组卷:324引用:2难度:0.7
6.如图,正六边形ABCDEF内接于⊙O,点G是EF弧上的一点,则∠BGA的度数为( )组卷:324引用:2难度:0.7 -
7.为丰富乡村文体生活,某区准备组织首届“美丽乡村”篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排28场比赛,设邀请x个球队参加比赛,可列方程得( )
组卷:1284引用:10难度:0.8 -
8.已知反比例函数
的图象在一、三象限,则化简代数式y=m-1x得( )(1-m)2组卷:318引用:3难度:0.7
三、解答题(本大题共9小题,满分72分,解答应写出文字说明、证明过程或演算步骤.)
-
24.已知,抛物线y=x2-(2m+2)x+m2+2m与x轴交于A,B两点(A在B的左侧).
(1)当m=0时,求点A,B坐标;
(2)若直线y=-x+b经过点A,且与抛物线交于另一点C,连接AC,BC,试判断△ABC的面积是否发生变化?若不变,请求出△ABC的面积;若发生变化,请说明理由;
(3)当5-2m≤x≤2m-1时,若抛物线在该范围内的最高点为M,最低点为N,直线MN与x轴交于点D,且,求此时抛物线的解析式.MDND=3组卷:878引用:3难度:0.2 -
25.如图1,射线OM⊥ON,点B在ON上,且OB=4,点A是射线OM上的动点.
(1)当OA=OB时,
①求∠ABO的度数;
②如图2,若P是∠MON内的一点,∠APB=90°且,求线段PO的长;PA+PB=52
(2)如图3以AB为直角边构造Rt△ABC,其中∠BAC=90°,且S△ABC=12,点D是线段BC的中点,点E与点A关于点D对称,连接OE,当线段OE取最大值时,求的值.ACAB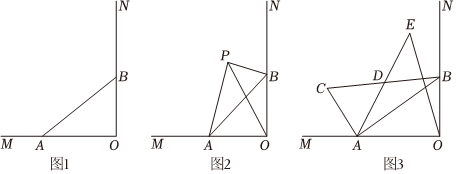 组卷:329引用:3难度:0.3
组卷:329引用:3难度:0.3


