2023-2024学年江苏省南京师大附中江宁分校八年级（上）月考数学试卷（10月份）

一、选择题（共10小题，每小题2分，共20分）

• 1．以下四家银行的行标图中，是轴对称图形的有（　　）
  

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：624引用：36难度：0.9

  解析

• 2．下列说法正确的是（　　）

  A．形状相同的两个三角形全等

  B．面积相等的两个三角形全等

  C．完全重合的两个三角形全等

  D．所有的等边三角形全等
  组卷：221引用：12难度：0.6

  解析

• 3．如图，已知AB⊥BC，BC⊥CD，AB=DC，则可以判定△ABC≌△DCB的根据是（　　）

  A．HL

  B．ASA

  C．SAS

  D．AAS
  组卷：188引用：2难度：0.8

  解析

• 4．在联欢会上，有A、B、C三名选手站在一个三角形的三个顶点位置上，他们在玩“抢凳子”游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置是在△ABC的（　　）

  A．三边垂直平分线的交点	B．三条中线的交点
  C．三条角平分线的交点	D．三条高所在直线的交点
  组卷：1271引用：47难度：0.6

  解析

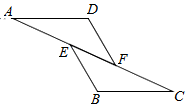• 5．如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（　　）

  A．∠B=∠D

  B．BE=DF

  C．AD=CB

  D．AD∥BC
  组卷：137引用：5难度：0.7

  解析

• 6．如图，DE是△ABC的边BC的垂直平分线，分别交边AB，BC于点D，E，且AB=9，AC=6，则△ACD的周长是（　　）

  A．10.5

  B．12

  C．15

  D．18
  组卷：2037引用：22难度：0.7

  解析

• 7．如图所示，已知AB=CD，AD=CB，AC、BD相交于O，则图中全等三角形有（　　）

  A．2对

  B．3对

  C．4对

  D．5对
  组卷：670引用：29难度：0.9

  解析

• 8．平面上有△ACD与△BCE，其中AD与BE相交于P点，如图．若AC=BC，AD=BE，CD=CE，∠ACE=55°，∠BCD=155°，则∠BPD的度数为（　　）

  A．110°

  B．125°

  C．130°

  D．155°
  组卷：5406引用：86难度：0.5

  解析

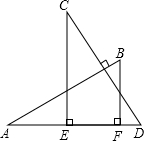• 9．如图，AB⊥CD，且AB=CD；E、F是AD上的两点，连接CE，BF，CE⊥AD，BF⊥AD，若CE=a,BF=b,EF=c,则AD的长为（　　）

  A．a-b+c

  B．a+b-c

  C．a+c

  D．b+c
  组卷：437引用：3难度：0.7

  解析

三、解答题（共7小题）

• 26．在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．
  （1）当直线MN绕点C旋转到图1的位置时，
  求证：①△ADC≌△CEB；
  ②DE=AD+BE；
  （2）当直线MN绕点C旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由．
  
  组卷：11315引用：37难度：0.3

  解析

• 27．【问题引领】
  
  问题1：如图1，在四边形ABCD中，CB=CD，∠B=∠ADC=90°，∠BCD=120°，E，F分别是AB，AD上的点，且∠ECF=60°．探究图中线段BE，EF，FD之间的数量关系．
  小王同学探究此问题的方法是，延长FD到点G．使DG=BE．连结CG，先证明△CBE≌△CDG，再证明△CEF≌△CGF．他得出的正确结论是

  ．
  【探究思考】
  问题2：如图2，若将问题1的条件改为：四边形ABCD中，CB=CD，∠ABC+∠ADC=180°，∠ECF=

  1

  2

  ∠BCD，问题1的结论是否仍然成立？请说明理由．
  【拓展延伸】
  问题3：如图3，在问题2的条件下，若点E在AB的延长线上，点F在DA的延长线上，若BE=2，DF=8，求EF的长．（请直接写出答案）
  组卷：345引用：4难度：0.1

  解析