2023-2024学年江苏省扬州市仪征市大仪中学九年级(上)第一次段考数学试卷
发布:2024/9/19 0:0:8
一.选择题(每小题3分,共24分。在每小题列出的选项中,选出符合题目的一项)
-
1.下列方程中,一定是关于x的一元二次方程的是( )
组卷:92引用:12难度:0.9 -
2.用配方法解方程x2-2x-5=0时,原方程应变形为( )
组卷:3939引用:792难度:0.9 -
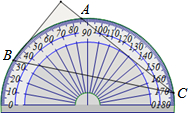 3.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )组卷:2229引用:164难度:0.9
3.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )组卷:2229引用:164难度:0.9 -
4.下列说法正确的是( )
组卷:290引用:38难度:0.7 -
5.在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )
组卷:10335引用:104难度:0.9 -
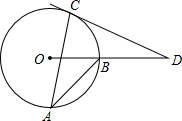 6.如图,AB、AC是⊙O的两条弦,∠A=25°,过点C的切线与OB的延长线交于点D,则∠D的度数( )组卷:323引用:8难度:0.7
6.如图,AB、AC是⊙O的两条弦,∠A=25°,过点C的切线与OB的延长线交于点D,则∠D的度数( )组卷:323引用:8难度:0.7 -
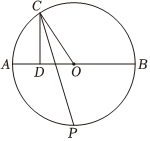 7.如图,AB为⊙O的直径,C为⊙O上的一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于P,则当C在⊙O上运动时,下列说法正确的是( )组卷:144引用:3难度:0.7
7.如图,AB为⊙O的直径,C为⊙O上的一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于P,则当C在⊙O上运动时,下列说法正确的是( )组卷:144引用:3难度:0.7 -
 8.如图,等边△ABC中,D在射线BA上,以CD为一边,向右上方作等边△EDC.若BC、CD的长为方程x2-15x+7m=0的两根,当m取符合题意的最大整数时,则不同位置的D点共有( )组卷:195引用:3难度:0.7
8.如图,等边△ABC中,D在射线BA上,以CD为一边,向右上方作等边△EDC.若BC、CD的长为方程x2-15x+7m=0的两根,当m取符合题意的最大整数时,则不同位置的D点共有( )组卷:195引用:3难度:0.7
二.填空题(本大题共10小题,每小题3分,共30分)
-
9.在平面内,⊙O的直径为10cm,点P到圆心O的距离是6cm,则点P与⊙O的位置关系是 .
组卷:252引用:10难度:0.9
三、解答题(本大题共10小题,共96.0分).
-
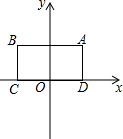 27.对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为(,2),顶点C、D在x轴上,且OC=OD.3
27.对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为(,2),顶点C、D在x轴上,且OC=OD.3
(1)当⊙P的半径为4时,
①在P1(0,-3),P2(2,3),P3(-23,1)中可以成为矩形ABCD的“等距圆”的圆心的是;3
②如果点P在直线上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;y=-33x+1
(2)已知点P在y轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.组卷:101引用:6难度:0.1 -
28.阅读材料:如图1,若点P是⊙O外的一点,线段PO交⊙O于点A,则PA长是点P与⊙O上各点之间的最短距离.
证明:延长PO交⊙O于点B,显然PB>PA.
如图2,在⊙O上任取一点C(与点A,B不重合),连接PC,OC.
∵PO<PC+OC,
且PO=PA+OA,OA=OC,
∴PA<PC
∴PA长是点P与⊙O上各点之间的最短距离.
由此可以得到真命题:圆外一点与圆上各点之间的最短距离是这点到圆心的距离与半径的差.请用上述真命题解决下列问题.
(1)如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,则AP长的最小值是.ˆCD
(2)如图4,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,①求线段A′M的长度; ②求线段A′C长的最小值.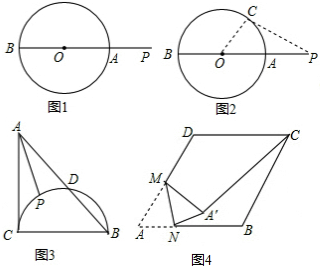 组卷:1530引用:5难度:0.5
组卷:1530引用:5难度:0.5


