2022-2023学年四川省成都七中九年级（上）第三次质检数学试卷

一、选择题（共8小题，每小题4分，满分32分）

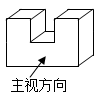
• 1．如图是一个“凹”字形几何体，这个几何体的俯视图是（　　）
  

  A．

  B．

  C．

  D．
  组卷：162引用：6难度：0.8

  解析

• 2．在“双创”期间，老师将全班分成7个小组开展“文明督导”活动，采用随机抽签法确定一个小组进行展示活动．则第3小组被抽到的概率是（　　）

  A． 1 21

  B． 1 10

  C． 1 7

  D． 1 3
  组卷：89引用：2难度：0.6

  解析

• 3．一元二次方程4x²-2x+

  1

  4

  =0的根的情况是（　　）

  A．有两个相等的实数根	B．有两个不相等的实数根
  C．只有一个实数根	D．没有实数根
  组卷：147引用：7难度：0.9

  解析

• 4．若2a=5b（a≠0），

  a

  +

  b

  a

  -

  b

  值为（　　）

  A． - 3 7

  B． 3 7

  C． 3 5

  D． 7 3
  组卷：22引用：1难度：0.8

  解析

• 5．高4米的旗杆在水平地面上的影长为6米，此时测得附近一个建筑物的影长24米，则该建筑物的高度为（　　）

  A．10米

  B．16米

  C．26米

  D．36米
  组卷：416引用：4难度：0.5

  解析

• 6．若反比例函数y=

  k

  x

  （k≠0）的图象经过点（-2，5），则这个函数的图象一定经过点（　　）

  A．（5，-1）

  B．（- 1 5 ，2）

  C．（-2，-5）

  D．（ 1 2 ，-20）
  组卷：640引用：5难度：0.5

  解析

• 7．已知α为锐角，且

  sin

  （

  α

  -

  10

  °

  ）

  =

  3

  2

  ，则α等于（　　）

  A．70°

  B．60°

  C．40°

  D．30°
  组卷：1342引用：6难度：0.7

  解析

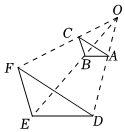• 8．如图，△ABC和△DEF是以点O为位似中心的位似图形，若OA：AD=2：3，则△ABC与△DEF的周长比是（　　）

  A．2：3

  B．3：2

  C．2：5

  D．5：2
  组卷：668引用：12难度：0.5

  解析

三、解答题（共13小题，满分98分）

• 25．已知反比例函数y=

  2

  x

  与直线l：y=kx-k（k≠0）相交于A、B两点，其中x_A＞x_B．
  （1）如图1，若k=1时，点A坐标为

  ；点B坐标为

  ；
  （2）在（1）的条件下，点C为双曲线y=

  2

  x

  第一象限上一点，若△ABC的面积为3，求点C的坐标；
  （3）如图2，点E坐标为（-2，0），连接AE，BE，是否存在直线l,使得△ABE是以AB为斜边的直角三角形？若存在，求出直线l的解析式；若不存在，请说明理由．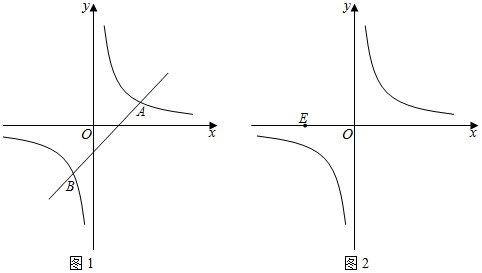
  
  组卷：795引用：2难度：0.2

  解析

• 26．在△ABC中，AC=BC=10，tanA=

  3

  4

  ，点D，E分别是AB，AC边上的动点，连接DE，作△ADE关于DE对称的图形△A′DE．
  （1）如图1，当点A′恰好与点C重合，求DE的长；
  （2）如图2，E是AC边的中点，当△A′DE是等腰三角形时，求AD的长；
  （3）如图3，E是AC边的中点，连接A′B，F是A′B的中点，连接CF，在D点的运动过程中，求线段CF长度的最大值．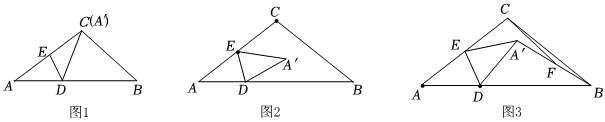
  
  组卷：122引用：2难度：0.3

  解析