2022-2023学年浙江省宁波市九校联考高二(下)期末数学试卷
发布:2024/5/19 8:0:9
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知复数z满足z•i=1+i,则
对应的点位于( )z组卷:30引用:3难度:0.8 -
2.设集合M={(x,y)|y=|2x-1|},
,则M∩N中元素的个数为( )N={(x,y)|y=cosπ2x,-4≤x≤4}组卷:26引用:2难度:0.6 -
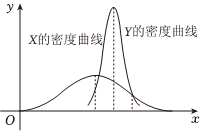 3.已知随机变量,X~N(μ1,σ21),它们的分布密度曲线如下图所示,则下列说法中正确的是( )Y~N(μ2,σ22)组卷:71引用:2难度:0.8
3.已知随机变量,X~N(μ1,σ21),它们的分布密度曲线如下图所示,则下列说法中正确的是( )Y~N(μ2,σ22)组卷:71引用:2难度:0.8 -
4.已知平面向量
,a满足b,则|a+b|=|a-b|在b-a上的投影向量为( )a组卷:90引用:4难度:0.8 -
5.若sin(α+
)=π4,α∈(0,π),则cos2α=( )13组卷:148引用:2难度:0.7 -
6.在△ABC中,点O满足
,过点O的直线分别交射线AB,AC于点M,N,且CO=2OB,AM=mAB,则m+2n的最小值为( )AN=nAC组卷:190引用:3难度:0.5 -
7.已知f(x)是定义在R上的奇函数,且f(2)=2,若对任意的x1,x2∈(0,+∞),均有
成立,则不等式f(x-1)+1>x的解集为( )f(x1)-f(x2)x1-x2>1组卷:163引用:3难度:0.5
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
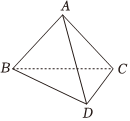 21.如图,四面体ABCD中,平面ABC⊥平面BCD,AB⊥AC,,CD=1.AB=AC=2
21.如图,四面体ABCD中,平面ABC⊥平面BCD,AB⊥AC,,CD=1.AB=AC=2
(1)若AD⊥AB,证明:CD⊥平面ABC;
(2)设过直线AD且与直线BC平行的平面为α,当BD与平面ABC所成的角最大时,求平面α与平面BCD的夹角.组卷:48引用:1难度:0.5 -
 22.已知f(x)=x+1,g(x)=x2+2.定义,设m(x)=min{f(|x-t|),g(|x-2t|)},t∈R.min{a,b}=a,a≤bb,b≤a
22.已知f(x)=x+1,g(x)=x2+2.定义,设m(x)=min{f(|x-t|),g(|x-2t|)},t∈R.min{a,b}=a,a≤bb,b≤a
(1)若t=3,(i)画出函数m(x)的图象;
(ii)直接写出函数m(x)的单调区间;
(2)定义区间A=(p,q)的长度L(A)=q-p.若,Ai∩Aj=∅(1≤i<j≤n),则B=A1∪A2∪⋯∪An(n∈N*).设关于x的不等式m(x)<t的解集为D.是否存在t,使得L(D)=6?若存在,求出t的值;若不存在,请说明理由.L(B)=n∑i=1L(Ai)组卷:15引用:3难度:0.4


