2022-2023学年福建省泉州外国语实验学校八年级（上）第一次月考数学试卷

一.选择题（共10小题）

• 1．如图，∠1=∠2，∠3=∠4，则判定△ABD和△ACD全等的依据是（　　）

  A．SSS

  B．ASA

  C．SAS

  D．HL
  组卷：1154引用：12难度：0.6

  解析

• 2．如图，∠C=∠F=90°，下列条件中，不能判定△ACB与△DFE全等的是（　　）

  A．∠A=∠D，AB=DE	B．AC=DF，BC=EF
  C．AB=DE，BC=EF	D．∠A=∠D，∠B=∠E
  组卷：12引用：1难度：0.6

  解析

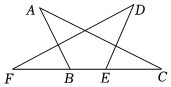• 3．如图，点F，B，E，C在同一条直线上，△ABC≌△DEF，若∠A=36°，∠F=24°，则∠DEC的度数为（　　）

  A．50°

  B．60°

  C．65°

  D．120°
  组卷：1146引用：8难度：0.7

  解析

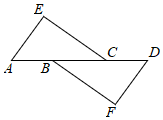• 4．如图，△ACE≌△DBF，若AD=11cm,BC=5cm,则AB长为（　　）

  A．6cm

  B．7cm

  C．4cm

  D．3cm
  组卷：950引用：10难度：0.6

  解析

• 5．如图，直线a、b分别经过等边三角形ABC的顶点A、C，且a∥b,∠1=42°，则∠2的度数为（　　）

  A．18°

  B．42°

  C．60°

  D．102°
  组卷：642引用：9难度：0.8

  解析

• 6．如图，A、B两点分别位于一个池塘的两端，小明想用绳子测量A、B间的距离，如图所示的这种方法，是利用了三角形全等中的（　　）

  A．SSS

  B．ASA

  C．AAS

  D．SAS
  组卷：1397引用：8难度：0.9

  解析

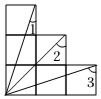• 7．如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=（　　）

  A．90°

  B．120°

  C．135°

  D．150°
  组卷：5798引用：41难度：0.9

  解析

• 8．如图，正方形的网格中，点A，B是小正方形的顶点，如果C点是小正方形的顶点，且使△ABC是等腰三角形，则点C的个数为（　　）

  A．6

  B．7

  C．8

  D．9
  组卷：1206引用：6难度：0.5

  解析

三.解答题（共9小题）

• 24．综合与探究
  如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，CE的延长线交BD于点F．
  （1）求证：△ACE≌△ABD．
  （2）若∠BAC=∠DAE=50°，请直接写出∠BFC的度数．
  （3）过点A作AH⊥BD于点H，求证：EF+DH=HF．
  组卷：2651引用：5难度：0.3

  解析

• 25．已知：如图所示，直线MA∥NB，∠MAB与∠NBA的平分线交于点C，过点C作一条直线l与两条直线MA、NB分别相交于点D、E．
  
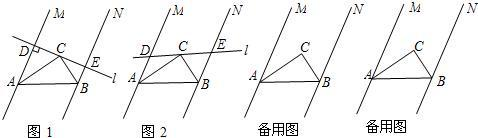
  （1）如图1所示，当直线l与直线MA垂直时，猜想线段AD、BE、AB之间的数量关系，请直接写出结论，不用证明；
  （2）如图2所示，当直线l与直线MA不垂直且交点D、E都在AB的同侧时，（1）中的结论是否成立？如果成立，请证明；如果不成立，请说明理由；
  （3）当直线l与直线MA不垂直且交点D、E在AB的异侧时，（1）中的结论是否仍然成立？如果成立，请说明理由；如果不成立，那么线段AD、BE、AB之间还存在某种数量关系吗？如果存在，请直接写出它们之间的数量关系．
  组卷：6512引用：24难度：0.1

  解析