2020-2021学年福建省南平市建瓯市房道中学九年级(上)月考数学试卷(10月份)
发布:2024/8/17 2:0:1
一、选择题
-
1.16的平方根是( )
组卷:107引用:16难度:0.9 -
2.方程2x2-6x=9的二次项系数、一次项系数、常数项分别为( )
组卷:3218引用:39难度:0.9 -
3.抛物线y=(x-2)2-3的顶点坐标是( )
组卷:1784引用:30难度:0.9 -
4.下列一元二次方程有两个相等的实数根的是( )
组卷:393引用:10难度:0.8 -
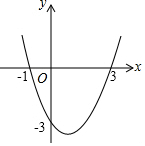 5.如图是一条抛物线的图象,则其解析式为( )组卷:4521引用:15难度:0.5
5.如图是一条抛物线的图象,则其解析式为( )组卷:4521引用:15难度:0.5 -
6.直角三角形两条直角边的和为7,面积是6,则斜边长是( )
组卷:811引用:23难度:0.9 -
7.把160元的电器连续两次降价后的价格为y元,若平均每次降价的百分率是x,则y与x的函数关系式为( )
组卷:1919引用:19难度:0.9 -
8.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )
组卷:4734引用:128难度:0.7
三、解答题
-
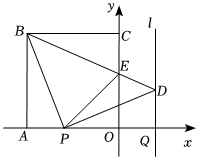 24.如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
24.如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
(1)写出∠PBD的度数和点D的坐标(点D的坐标用t表示);
(2)探索△POE周长是否随时间t的变化而变化,若变化,说明理由;若不变,试求这个定值.
(3)当t为何值时,△PBE为等腰三角形?组卷:703引用:8难度:0.5 -
25.已知直线l:y=-2,抛物线C:y=ax2-1经过点(2,0)
(1)求a的值;
(2)如图①,点P是抛物线C上任意一点,过点P作直线l的垂线,垂足为Q.求证:PO=PQ;
(3)请你参考(2)中的结论解决下列问题
1.如图②,过原点作直线交抛物线C于A,B两点,过此两点作直线l的垂线,垂足分别为M,N,连接ON,OM,求证:OM⊥ON;
2.如图③,点D(1,1),使探究在抛物线C上是否存在点F,使得FD+FO取得最小值?若存在,求出点F的坐标,若不存在,请说明理由.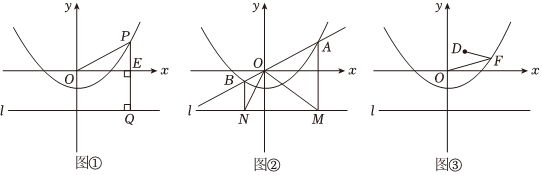 组卷:412引用:5难度:0.3
组卷:412引用:5难度:0.3


