2022-2023学年广东省河源市龙川第一实验学校八年级（下）开学数学试卷

一、单选题：本大题共10小题，每小题3分，共30分。

• 1．若m,n是一元二次方程x²-2x-1=0的两个不同实数根，则代数式m²-m+n的值是（　　）

  A．-1

  B．3

  C．-3

  D．1
  组卷：414引用：10难度：0.7

  解析

• 2．下列方程是关于x的一元二次方程的是（　　）

  A． x 2 + 1 x = 1	B．ax2+bx+c=0
  C．（x+1）（x+2）=1	D．3x2-2xy-5y=0
  组卷：287引用：7难度：0.8

  解析

• 3．从正面观察如图的两个立体图形，得到的平面图形是（　　）

  A．

  B．

  C．

  D．
  组卷：1780引用：24难度：0.9

  解析

• 4．已知关于x的方程x²-kx-6=0的一个根为x=3，则实数k的值为（　　）

  A．1

  B．-1

  C．2

  D．-2
  组卷：2342引用：205难度：0.9

  解析

• 5．方程x²-x=0的解为（　　）

  A．x1=x2=1

  B．x1=x2=0

  C．x1=0，x2=1

  D．x1=1，x2=-1
  组卷：833引用：9难度：0.6

  解析

• 6．方程x（x-2）=0的解是（　　）

  A．0

  B．2

  C．0 或 2

  D．无解
  组卷：30引用：3难度：0.9

  解析

• 7．若（m²-4）x²+3x-5=0是关于x的一元二次方程，则（　　）

  A．m≠2	B．m≠-2
  C．m≠-2，或 m≠2	D．m≠-2，且 m≠2
  组卷：136引用：2难度：0.8

  解析

• 8．若关于x的一元二次方程x²+2（k-1）x+k²-1=0有实数根，则k的取值范围是（　　）

  A．k≥1

  B．k＞1

  C．k＜1

  D．k≤1
  组卷：2080引用：19难度：0.7

  解析

三、解答题：第18，19.20小题6分，第21，22，23小题9分，第24，25小题10分。

• 24．现有正方形ABCD和一个以O为直角顶点的三角板，移动三角板，使三角板的两直角边所在直线分别与直线BC，CD交于点M，N．如图1，若点O与点A重合，容易得到线段OM与ON的关系，
  
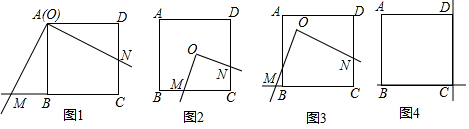
  （1）观察猜想：如图2，若点O在正方形的中心（即两条对角线的交点），OM与ON的数量关系是

   

  ；
  （2）探究证明；如图3，若点O在正方形的内部（含边界），且OM=ON，请判断三角板移动过程中所有满足条件的点O可组成什么图形，并说明理由；
  （3）拓展延伸：若点O在正方形的外部，且OM=ON，请你在图4中画出满足条件的一种情况，并就“三角板在各种情况下（含外部）移动，所有满足条件的点O所组成的图形”，写出正确的结论（不必说明理由）．
  组卷：443引用：5难度：0.1

  解析

• 25．如图，正方形OABC的顶点O是坐标原点，边OA和OC分别在x轴、y轴上，点B的坐标为（4，4）．直线l经过点C．
  （1）若直线l与边OA交于点M，过点A作直线l的垂线，垂足为D，交y轴于点E．
  ①如图1，当OE=1时，求直线l对应的函数表达式；
  ②如图2，连接OD，求证：OD平分∠CDE．
  （2）如图3，若直线l与边AB交于点P，且S_△BCP=

  1

  3

  S_{四边形AOCP}，此时，在x轴上是否存在点Q，使△CPQ是以CP为直角边的直角三角形？若存在，求点Q的坐标，若不存在，请说明理由．
  
  组卷：957引用：5难度：0.3

  解析