2019-2020学年新疆乌鲁木齐九中九年级（上）第二次月考数学试卷

一、单选题（每小题5分，共45分）

• 1．观察下列图形，既是轴对称图形又是中心对称图形的有（　　）
  

  A．1个

  B．2个

  C．3个

  D．4个
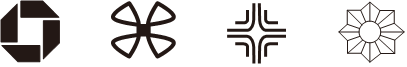  组卷：298引用：72难度：0.9

  解析

• 2．二次函数y=-3（x+1）²-2的顶点坐标是（　　）

  A．（-1，-2）

  B．（-1，2）

  C．（1，-2）

  D．（1，2）
  组卷：1856引用：21难度：0.9

  解析

• 3．把抛物线y=5x²向左平移2个单位，再向上平移3个单位，得到的抛物线是（　　）

  A．y=5（x-2）2+3	B．y=5（x+2）2-3
  C．y=5（x+2）2+3	D．y=5（x-2）2-3
  组卷：2600引用：47难度：0.8

  解析

• 4．若二次函数y=x²-6x+c的图象过A（-1，y₁），B（3，y₂），C（3+

  2

  ，y₃），则y₁，y₂，y₃的大小关系是（　　）

  A．y1＞y2＞y3

  B．y1＞y3＞y2

  C．y2＞y1＞y3

  D．y3＞y1＞y2
  组卷：572引用：8难度：0.9

  解析

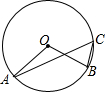• 5．如图，OA，OB是⊙O的半径，点C在⊙O上，连接AC，BC，若∠A=20°，∠B=70°，则∠ACB的度数为（　　）

  A．50°

  B．55°

  C．60°

  D．65°
  组卷：352引用：16难度：0.9

  解析

• 6．在同一坐标系中，抛物线y=4x²，y=

  1

  4

  x²，y=-

  1

  4

  x²的共同特点是（　　）

  A．关于y轴对称，开口向上

  B．关于y轴对称，y随x的增大而增大

  C．关于y轴对称，y随x的增大而减小

  D．关于y轴对称，顶点是原点
  组卷：954引用：32难度：0.9

  解析

• 7．抛物线y=-x²+bx+c上部分点的横坐标x,纵坐标y的对应值如下表：
  

  x	…	-2	-1	0	1	2	…
  y	…	0	4	6	6	4	…

  从上表可知，下列说法正确的个数是（　　）
  ①抛物线与x轴的一个交点为（-2，0）；
  ②抛物线与y轴的交点为（0，6）；
  ③抛物线的对称轴是直线x=1；
  ④在对称轴左侧y随x增大而增大．

  A．1

  B．2

  C．3

  D．4
  组卷：1032引用：59难度：0.9

  解析

• 8．抛物线y=-x²+4x-4与坐标轴的交点个数为（　　）

  A．0

  B．1

  C．2

  D．3
  组卷：3681引用：32难度：0.9

  解析

三、解答题（共75分）

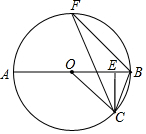• 23．已知，如图，AB为⊙O的直径，点C是半圆上一点，CE⊥AB于E，BF∥OC，连接BC，CF．
  （1）求证：∠OCF=∠ECB；
  （2）当AB=10，BC=2

  5

  ，求CF的值．
  组卷：404引用：5难度：0.4

  解析

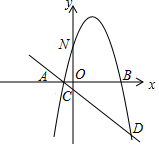• 24．如图，抛物线y=-x²+bx+c与x轴交于A、B两点（A在B的左侧），与y轴交于点N，过A点的直线l：y=kx+n与y轴交于点C，与抛物线y=-x²+bx+c的另一个交点为D，已知A（-1，0），D（5，-6），P点为抛物线y=-x²+bx+c上一动点（不与A、D重合）．
  （1）求抛物线和直线l的解析式；
  （2）当点P在直线l上方的抛物线上时，过P点作PE∥x轴交直线l于点E，作PF∥y轴交直线l于点F，求PE+PF的最大值；
  （3）设M为直线l上的点，探究是否存在点M，使得以点N、C，M、P为顶点的四边形为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．
  组卷：3722引用：17难度：0.4

  解析