2023-2024学年云南省昆明十中教育集团九年级(上)期中数学试卷
发布:2024/9/21 14:0:9
一.选择题(每题3分,共36分)
-
1.如图汽车标志中,是中心对称图形的是( )
组卷:22引用:3难度:0.9 -
2.已知圆O的半径为5,同一平面内有一点P,且OP=4,则点P与圆O的关系是( )
组卷:389引用:8难度:0.5 -
3.将抛物线y=x2+2向左平移3个单位长度,再向下平移4个单位长度得到的抛物线解析式为( )
组卷:343引用:3难度:0.5 -
4.关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
组卷:6793引用:91难度:0.7 -
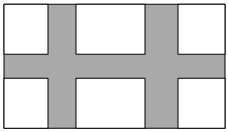 5.如图,某小区居民休闲娱乐中心是建在一块长方形(长30米,宽20米)场地,被3条宽度相等的绿化带划分为总面积为480平方米的6块活动场所.如果想求绿化带的宽度x米,可列出的方程为( )组卷:707引用:2难度:0.5
5.如图,某小区居民休闲娱乐中心是建在一块长方形(长30米,宽20米)场地,被3条宽度相等的绿化带划分为总面积为480平方米的6块活动场所.如果想求绿化带的宽度x米,可列出的方程为( )组卷:707引用:2难度:0.5 -
6.已知点(-2,y1),(-1,y2),(5,y3)都在函数y=(x-3)2+1的图象上,则( )
组卷:190引用:5难度:0.5 -
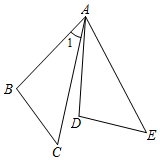 7.如图,把△ABC绕点A逆时针旋转40°得到△ADE,∠1=30°,则∠BAE=( )组卷:147引用:5难度:0.8
7.如图,把△ABC绕点A逆时针旋转40°得到△ADE,∠1=30°,则∠BAE=( )组卷:147引用:5难度:0.8 -
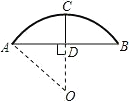 8.如图,有一圆弧形桥拱,拱形的半径OA=10m,桥拱的跨度AB=16m,则拱高CD为( )组卷:1011引用:11难度:0.9
8.如图,有一圆弧形桥拱,拱形的半径OA=10m,桥拱的跨度AB=16m,则拱高CD为( )组卷:1011引用:11难度:0.9
三.解答题(共56分)
-
23.综合与实践:
“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.
提出问题:
如图1所示,在线段AC同侧有两点B,D,连接AD,AB,BC,CD,如果∠B=∠D,那么A,B,C,D四点在同一个圆上.
探究展示:
如图2所示,作经过点A,C,D的⊙O,在劣弧AC上取一点E(不与A,C重合),连接AE,CE,则∠AEC+∠D=180°,(依据1)
∵∠B=∠D,
∴∠AEC+∠B=180°,
∴点A,B,C,E四点在同一个圆上,(对角互补的四边形四个顶点共圆)
∴点B,D在点A,C,E所确定的⊙O上,(依据2)
∴点A,B,C,D四点在同一个圆上;
反思归纳:
(1)上述探究过程中的“依据1”、“依据2”分别是指什么?①圆内接四边形对角互补;
②对角互补的四边形四个顶点共圆;
③过不在同一直线上的三个点有且只有一个圆;
④经过两点的圆的圆心在这两点所连线段的垂直平分线上;
依据1:;(从框内选一个选项,直接填序号)
依据2:.(从框内选一个选项,直接填序号)
(2)如图3所示,在四边形ABCD中,∠1=∠2=80°,∠3=42°,则∠4的度数为 .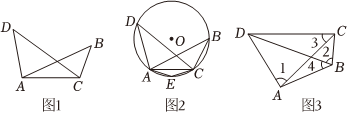 组卷:279引用:1难度:0.4
组卷:279引用:1难度:0.4 -
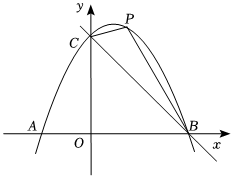 24.如图,抛物线y=ax2+x+c与x轴交于A,B两点(点A在点B的左侧),且点B为(4,0),与y轴交于点C(0,4),直线BC经过B,C两点,点P是第一象限内抛物线上的一个动点,连接PB,PC.
24.如图,抛物线y=ax2+x+c与x轴交于A,B两点(点A在点B的左侧),且点B为(4,0),与y轴交于点C(0,4),直线BC经过B,C两点,点P是第一象限内抛物线上的一个动点,连接PB,PC.
(1)求抛物线的函数表达式;
(2)直线BC的解析式记为y1=kx+b,当y>y1时,直接写出x的取值范围;
(3)设点P的横坐标为n,四边形OBPC的面积为S,求S的最大值并求出此时点P的坐标.组卷:198引用:1难度:0.4


