2023-2024学年江西省南昌三中教育集团八年级(上)期中数学试卷
发布:2024/10/4 2:0:2
一、选择题(本大题共6小题,共18分。在每小题列出的选项中,选出符合题目的一项)
-
1.一个五边形的内角和为( )
组卷:1133引用:8难度:0.9 -
2.用两根8cm,17cm长的木棒做一个三角形,可以选用第三根木棒的长为( )
组卷:34引用:2难度:0.7 -
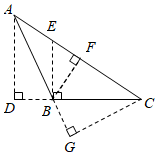 3.如图,在△ABC中,BC边上的高为( )组卷:2430引用:24难度:0.6
3.如图,在△ABC中,BC边上的高为( )组卷:2430引用:24难度:0.6 -
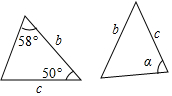 4.如图,两个三角形为全等三角形,则∠α的度数是( )组卷:1575引用:11难度:0.9
4.如图,两个三角形为全等三角形,则∠α的度数是( )组卷:1575引用:11难度:0.9 -
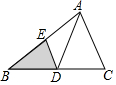 5.如图,已知△ABC中,点D、E分别是边BC、AB的中点.若△ABC的面积等于8,则△BDE的面积等于( )组卷:4847引用:23难度:0.7
5.如图,已知△ABC中,点D、E分别是边BC、AB的中点.若△ABC的面积等于8,则△BDE的面积等于( )组卷:4847引用:23难度:0.7 -
 6.如图,△ABC中,AB=AC,∠B=∠C=40°,D为线段BC上一动点(不与点B,C重合),连接AD,作∠ADE=40°,DE交线段AC于E,以下四个结论:①∠CDE=∠BAD;②当AB=CD时,△ABD≌△DCE;③当△ADE为等腰三角形时,∠BAD=20°;④当∠BAD=30°时,BD=CE.其中正确的结论的个数是( )组卷:33引用:1难度:0.7
6.如图,△ABC中,AB=AC,∠B=∠C=40°,D为线段BC上一动点(不与点B,C重合),连接AD,作∠ADE=40°,DE交线段AC于E,以下四个结论:①∠CDE=∠BAD;②当AB=CD时,△ABD≌△DCE;③当△ADE为等腰三角形时,∠BAD=20°;④当∠BAD=30°时,BD=CE.其中正确的结论的个数是( )组卷:33引用:1难度:0.7
二、填空题(本大题共6小题,共18分)
-
 7.随着人们物质生活的提高,手机成为一种生活中不可缺少的东西,手机很方便携带,但唯一的缺点就是没有固定的支点.为了解决这一问题,某工厂研制生产了一种如图所示的手机支架.把手机放在上面就可以方便地使用手机,这是利用了三角形的 .组卷:176引用:9难度:0.6
7.随着人们物质生活的提高,手机成为一种生活中不可缺少的东西,手机很方便携带,但唯一的缺点就是没有固定的支点.为了解决这一问题,某工厂研制生产了一种如图所示的手机支架.把手机放在上面就可以方便地使用手机,这是利用了三角形的 .组卷:176引用:9难度:0.6
五、综合题(本大题共2小题,共18分。解答应写出文字说明,证明过程或演算步骤)
-
22.已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;
(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.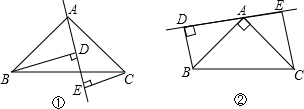 组卷:436引用:14难度:0.3
组卷:436引用:14难度:0.3
六、解答题(本大题共1小题,共12分。解答应写出文字说明,证明过程或演算步骤)
-
23.(1)如图1,在△ABC中,AB=4,AC=6,AD是BC边上的中线,延长AD到点E使DE=AD,连接CE,把AB,AC,2AD集中在△ACE中,利用三角形三边关系可得AD的取值范围是 ;
(2)如图2,在△ABC中,AD是BC边上的中线,点E,F分别在AB,AC上,且DE⊥DF,求证:BE+CF>EF;
(3)如图3,在四边形ABCD中,∠A为钝角,∠C为锐角,∠B+∠ADC=180°,DA=DC,点E,F分别在BC,AB上,且∠EDF=∠ADC,连接EF,试探索线段AF,EF,CE之间的数量关系,并加以证明.12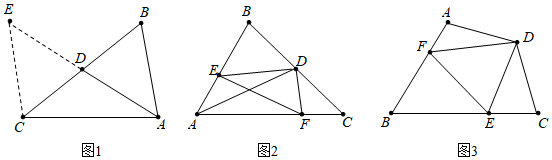 组卷:1639引用:9难度:0.1
组卷:1639引用:9难度:0.1


