2020-2021学年安徽省阜阳师范学院附中八年级（上）月考数学试卷（10月份）
发布：2024/7/26 8:0:9
一．选择题（每小题4分，共40分）
-
1．如图，图中三角形的个数为（ ）组卷：1046引用：9难度：0.9 -
2．下面分别是三根小木棒的长度，能摆成三角形的是（ ）
组卷：821引用：20难度：0.8 -
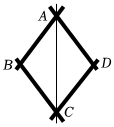3．如图是一个平分角的仪器，其中AB=AD，BC=DC，将点A放在角的顶点，AB和AD沿着角的两边放下，沿AC画一条射线，这条射线就是角的平分线，在这个操作过程中，运用了三角形全等的判定方法是（ ）组卷：3328引用：42难度：0.9 -
4．三角形的三个内角的度数之比为2：3：7，则这个三角形最大内角一定是（ ）
组卷：915引用：10难度：0.8 -
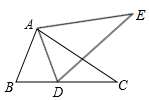
5．如图，若△ABC≌△ADE，则下列结论中一定成立的是（ ）
组卷：5338引用：81难度：0.8 -
6．已知等腰三角形的两边长分别为8cm、4cm,则这个三角形的周长为（ ）
组卷：372引用：17难度：0.9 -
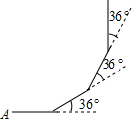7．如图，小明从A点出发，沿直线前进10米后向左转36°，再沿直线前进10米，再向左转36°……照这样走下去，他第一次回到出发点A点时，一共走的路程是（ ）组卷：1669引用：24难度：0.7
七．（本题12分）
-
22．已知△ABC中，∠ABC=∠ACB，D为线段CB上一点（不与C，B重合），点E为射线CA上一点，∠ADE=∠AED，设∠BAD=α，∠CDE=β．
（1）如图（1），
①若∠BAC=42°，∠DAE=30°，则α=，β=．
②若∠BAC=54°，∠DAE=36°，则α=，β=．
③写出α与β的数量关系，并说明理由；
（2）如图（2），当E点在CA的延长线上时，其它条件不变，请直接写出α与β的数量关系．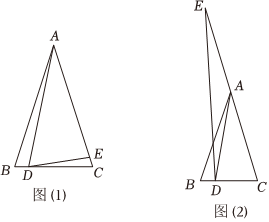
组卷：231引用：4难度：0.1
八．（本题14分）
-
23．已知△ABC，点D、F分别为线段AC、AB上两点，连接BD、CF交于点E．
（1）若BD⊥AC，CF⊥AB，如图1所示，试说明∠BAC+∠BEC=180°；
（2）若BD平分∠ABC，CF平分∠ACB，如图2所示，试说明此时∠BAC与∠BEC的数量关系；
（3）在（2）的条件下，若∠BAC=60°，试说明：EF=ED．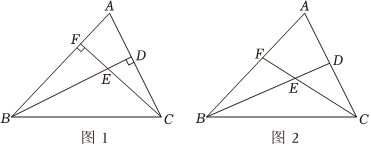
组卷：2865引用：16难度：0.5
