2022-2023学年陕西省西安市铁一中学、滨河中学、铁一陆港中学三校联考九年级(上)期末数学试卷
发布:2024/9/9 5:0:8
一、选择题(共8小题,每小题3分,共24分,每小题只有一个选项是符合题意的)
-
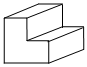 1.如图中几何体的左视图为( )组卷:414引用:2难度:0.9
1.如图中几何体的左视图为( )组卷:414引用:2难度:0.9 -
2.在Rt△ABC中,∠C=90°,BC=3,
,则tanA=( )sinA=35组卷:911引用:7难度:0.7 -
3.若
,则ab=34=( )a-ba+b组卷:783引用:5难度:0.8 -
4.在平面直角坐标系中,△AOB三个顶点的坐标分别为A(2,0),O(0,0),B(-1,1).以坐标原点O为位似中心,作与△AOB位似的△A'OB',使得△A'OB'与△AOB的相似比为2,则点B的对应点B'的坐标为( )
组卷:447引用:2难度:0.7 -
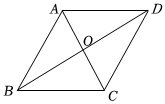 5.如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=6,DB=8,则点A到BC的距离为( )组卷:543引用:5难度:0.5
5.如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=6,DB=8,则点A到BC的距离为( )组卷:543引用:5难度:0.5 -
6.小明和小强晚上相约一起测量放学路上路灯的高度.小明将一个长为1米的木棒平行于地面放置在路灯下,小强测出此时木棒在路灯下影长为1.75米,且木棒距离地面的距离为1.5米,则路灯的高度为( )
组卷:218引用:1难度:0.7 -
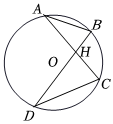 7.如图,AB、CD为⊙O的两条弦,⊙O的半径为r,AB=r,CD=r,连接AC、BD,AC与BD交于点H,则∠BHC的度数为( )2组卷:1112引用:2难度:0.5
7.如图,AB、CD为⊙O的两条弦,⊙O的半径为r,AB=r,CD=r,连接AC、BD,AC与BD交于点H,则∠BHC的度数为( )2组卷:1112引用:2难度:0.5 -
8.已知抛物线y=ax2-2ax+c(a,c为常数,且a>0),关于抛物线的下列说法中,不正确的是( )
组卷:560引用:3难度:0.4
三、解答题(共11小题,共78分,解答题写出过程)
-
24.已知抛物线C:y=2x2+bx+c(a≠0)与x轴交于O(0,0)、A(5,0).
(1)求抛物线C的表达式;
(2)将抛物线C平移得到抛物线C',其中A点平移后的对应点记为A',O点平移后的对应的点记为O',当以A、O、A'、O'为顶点的四边形为面积为20的菱形,且抛物线C'顶点在y轴的右侧时,求平移后得到的抛物线C'的表达式.组卷:458引用:2难度:0.3 -
25.如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为倍角三角形,并称这两个角的公共边为底边.
例如:若△ABC中,∠A=2∠B,则△ABC为以边AB为底边的倍角三角形.
问题提出
(1)已知△ABC为倍角三角形,且∠ABC=2∠C.
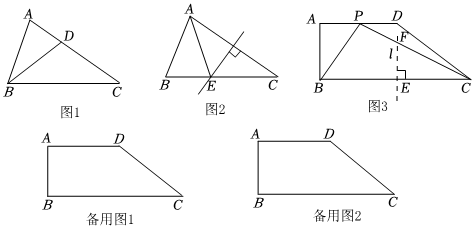
①如图1,若BD为△ABC的角平分线,则图中相等的线段有 ,图中相似三角形有 ;
②如图2,若AC的中垂线交边BC于点E,连接AE,则图中等腰三角形有 .
问题解决
(2)如图3,现有一块梯形板材ABCD,AD∥BC,∠A=90°,AB=48,BC=132,AD=68.工人师傅想用这块板材裁出一个△BCP型部件,使得点P在梯形ABCD的边上,且△BCP为以BC为底边的倍角三角形.工人师傅在这块板材上的作法如下:
①作BC的中垂线l交BC于点E;
②在BC上方的直线l上截取EF=33,连接CF并延长,交AD于点P;
③连接BP,得△BCP.
1)请问,若按上述作法,裁得的△BCP型部件是否符合要求?请证明你的想法.
2)是否存在其它满足要求的△BCP?若存在,请画出图形并求出CP的长;若不存在,请说明理由.组卷:316引用:1难度:0.2


