2023-2024学年广东省惠州市惠城区惠台学校九年级(上)开学数学试卷
发布:2024/8/5 8:0:8
一、选择题(本大题共10小题,每小题3分,共30分)
-
1.在平面直角坐标系内,把点P(-2,4)沿x轴方向向右平移一个单位,则得到的对应点P′的坐标是( )
组卷:349引用:5难度:0.5 -
2.下列不等式中不一定成立的是( )
组卷:1916引用:12难度:0.6 -
3.若分式
中的a、b的值同时扩大到原来的3倍,则分式的值( )2aba+b组卷:727引用:6难度:0.9 -
4.已知一次函数y=-x+2,那么下列结论正确的是( )
组卷:2205引用:17难度:0.5 -
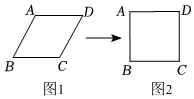 5.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )组卷:2493引用:27难度:0.5
5.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )组卷:2493引用:27难度:0.5 -
6.为计算某样本数据的方差,列出如下算式S2=
,据此判断下列说法错误的是( )(2-x)2+2(3-x)2+(7-x)2n组卷:241引用:4难度:0.7 -
7.若4x2-(k+1)x+9能用完全平方公式因式分解,则k的值为( )
组卷:3510引用:27难度:0.6
五、解答题(本大题共2小题,每小题12分,共24分)
-
22.【方法回顾】连接三角形任意两边中点的线段叫三角形的中位线,探索三角形中位线的性质,方法如下:如图1,D、E分别是AB、AC中点,延长DE到F,使EF=DE,连接CF;
(1)证明△ADE≌△CFE,再证四边形DBCF是平行四边形,从而得到线段DE与BC的位置关系和数量关系分别为 、.
(2)【初步运用】如图2,正方形ABCD中,E为边AD中点,G、F分别在边AB、CD上,且AG=2,DF=3,∠GEF=90°,求GF长.
(3)【拓展延伸】如图3,四边形ABCD中,∠A=100°,∠D=110°,E为AD中点,G、F分别为AB、CD边上的点,若AG=2,DF=,∠GEF=90°,求GF长.3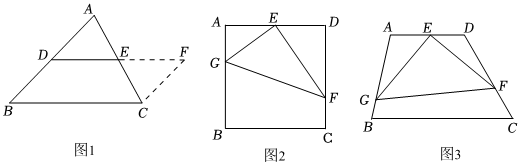 组卷:560引用:4难度:0.3
组卷:560引用:4难度:0.3 -
23.已知,如图①,在▱ABCD中,∠A=90°,AB=BC=4
,点E为CD上的一动点,连接BE,过点C作CH⊥BE于点H,以CH为腰作等腰直角△HCG,∠HCG=90°,连接DH.5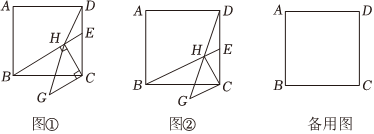
(1)求证:四边形ABCD为正方形;
(2)如图②,当D,H,G三点共线时,求DH2+DG2的值;
(3)求DH的最小值.组卷:627引用:3难度:0.4


