2022-2023学年湖北省武汉市洪山区鲁巷中学九年级（上）月考数学试卷（10月份）

一、选择题（共10小题，每小题3分，共30分）

• 1．在下列四个图案中，既是轴对称图形，又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：117引用：6难度：0.9

  解析

• 2．方程5x²-1=4x的二次项系数、一次项系数、常数项分别为（　　）

  A．5，-1，4

  B．5，-1，-4

  C．5，-4，-1

  D．5，4，-1
  组卷：84引用：6难度：0.7

  解析

• 3．把方程x²-6x+1=0转化成（x+m）²=n的形式，则m、n的值是（　　）

  A．3，8

  B．3，10

  C．-3，10

  D．-3，8
  组卷：93引用：5难度：0.7

  解析

• 4．关于x的一元二次方程2x²-3x=-x-1的根的情况是（　　）

  A．有两个不等的实数根	B．有两相等的实数根
  C．无实数根	D．无法判断
  组卷：28引用：3难度：0.5

  解析

• 5．某超市一月份的营业额为200万元，一月、二月、三月的营业额共1000万元，如果平均每月增长率为x,则根据题意列方程为（　　）

  A．200（1+x）2=1000

  B．200+200（1+x）2=1000

  C．200（1+x）3=1000

  D．200+200（1+x）+200（1+x）2=1000
  组卷：346引用：6难度：0.9

  解析

• 6．抛物线y=3x²-6x-3的图象向左平移2个单位，再向上平移2个单位，所得图象的解析式为y=3x²+bx+c,则b,c的值为（　　）

  A．b=6，c=-1

  B．b=-18，c=23

  C．b=6，c=-5

  D．b=-18，c=29
  组卷：262引用：6难度：0.5

  解析

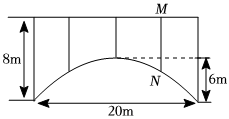• 7．一座拱桥的轮廓是抛物线型（如图所示），桥高为8米，拱高6米，跨度20米．相邻两支柱间的距离均为5米，则支柱MN的高度为（　　）米．

  A．2.5米

  B．3米

  C．3.5米

  D．4米
  组卷：249引用：4难度：0.5

  解析

• 8．若点A（-2，y₁），B（1，y₂），C（m,y₃）在抛物线y=2ax²+4ax+c上，且y₁＜y₃＜y₂，则m的取值范围是（　　）

  A．-3＜m＜-2	B．-3＜m＜-2或0＜m＜1
  C．m＜-3或m＞1	D．-3＜m＜0或-2＜m＜1
  组卷：51引用：3难度：0.6

  解析

三、解答题（共8小题，共72分）

• 23．如图，等边△ABC与等腰三角形△EDC有公共顶点C，其中∠EDC=120°，AB=CE=2

  6

  ，连接BE，P为BE的中点，连接PD、AD
  （1）为了研究线段AD与PD的数量关系，将图1中的△EDC绕点C旋转一个适当的角度，使CE与CA重合，如图2，请直接写出AD与PD的数量关系；
  （2）如图1，（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；
  （3）如图3，若∠ACD=45°，求△PAD的面积．
  
  组卷：1365引用：6难度：0.1

  解析

• 24．已知抛物线y=

  1

  4

  x²+bx+c的顶点（0，1）．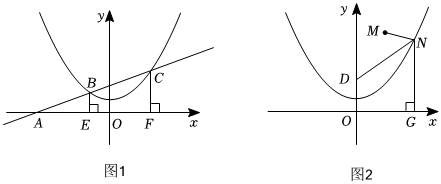
  
  （1）该抛物线的解析式为

  ；
  （2）如图1，直线y=kx+kt交x轴于A，交抛物线于B、C，BE⊥x轴于E，CF⊥x轴于F，试比较AE•AF与t²的大小关系．
  （3）如图2，D（0，2），M（2，5），点N是抛物线上一点，NG⊥x轴于G，
  ①求证：NG=ND；
  ②是否存在点N，使得NM+ND取得最小值，若存在，直接写出N的坐标和最小值，若不存在，说明理由．
  组卷：36引用：2难度：0.5

  解析