2023-2024学年山东省青岛市城阳区九年级（上）期中数学试卷
发布：2024/10/8 3:0:1
一、选择题（本大题共10小题，每小题3分，共30分）在每小题给出的四个选项中，只有一项是符合题目要求的.
-
1．方程x2=2x的解是（ ）
组卷：266引用：66难度：0.9 -
2．若四条线段a,b,c,d成比例，其中a=2cm,b=4cm,d=6cm,则线段c的长为（ ）
组卷：93引用：1难度：0.5 -
3．菱形具有而矩形不一定具有的性质是（ ）
组卷：2060引用：108难度：0.9 -
4．用图中两个可自由转动的转盘做“配紫色”游戏：分别旋转两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色．那么可配成紫色的概率是（ ）组卷：1850引用：26难度：0.5 -
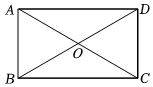5．如图，矩形ABCD中，对角线AC、BD交于点O．若∠AOB=60°，BD=8，则AB的长为（ ）组卷：2071引用：31难度：0.8 -
6．某商场品牌手机经过5，6月份连续两次降价每部售价由5000元降到3600元．且第一次降价的百分率是第二次的2倍，设第二次降价的百分率为x,根据题意可列方程（ ）
组卷：1494引用：7难度：0.5 -
7．如图，“笔尖”图案五边形ABECD由正方形ABCD和等边△BCE组成，连接AE，DE，则∠AED的度数为（ ）组卷：210引用：2难度：0.6 -
8．输入一组数据，按下列程序进行计算，输出结果如表：
分析表格中的数据，估计方程（x+8）2-826=0的一个正数解x的大致范围为（ ）x 20.5 20.6 20.7 20.8 20.9 输出 -13.75 -8.04 -2.31 3.44 9.21 组卷：1849引用：31难度：0.7
四、解答题（本大题共9小题，满分68分）
-
25．【问题提出】有编号分别为1，2，3，…，n（n为正整数，且n≥1）的n个球，甲、乙轮流抓，每次可以抓1个球或相连编号的2个球．甲先抓，规定谁抓到最后一次谁获胜．甲第1次应该怎样抓才能获胜？
【问题探究】我们采取一般问题特殊化的策略，先从最简单的情形入手，再逐次递进，从中找规律．
（1）如图①，当n=1时，甲一次抓一个球就可以抓完，显然甲获胜；
（2）如图②，当n=2时，甲一次抓编号相连的1号和2号2个球就可以抓完，所以甲获胜；
（3）如图③，当n=3时，甲第1次先抓2号球，乙第1次无论抓1号球还是3号球，最后还剩1个球，甲第2次抓就可以抓完，所以甲获胜；
（4）如图④，当n=4时，甲第1次先抓编号相连的2号和3号球，乙第1次无论抓1号球还是4号球，最后还剩1个球，甲第2次抓就可以抓完，所以甲获胜；
（5）如图⑤，当n=5时，甲第1次先抓3号球，乙第1次抓有两类抓法：一类：一次抓1个球．若乙第1次从1号和2号中任抓1个球，则甲第2次从4号和5号中任抓1个球，乙第2次无论抓那个球，最后还剩1个球，甲第3次抓就可以抓完，甲获胜．同理，若乙第1次从4号和5号中任抓1个球，甲也会获胜．二类：一次抓相连编号的2个球．若乙第1次抓编号相连的1号和2号球，则甲第2次抓编号相连的4号和5号球就可以抓完，甲获胜．同理，若乙第1次抓编号相连的4号和5号球，甲也会获胜．
（6）如图⑥，当n=6时，甲第1次应该怎样抓第1次应该抓 号球；
（7）如图⑦，当n=7时，甲要获胜，第1次应该抓 号球；
【问题解决】有编号分别为1，2，3，…，n（n为正整数，且n≥1）的n个球，甲、乙轮流抓，每次可以抓1个球或相连编号的2个球．甲先抓，规定谁抓到最后一次谁获胜．甲第1次应该怎样抓才能获胜？（只写出结论）
【拓展应用】有编号分别为1，2，3，…，（n为正整数，且n≥1）的n个球，甲、乙轮流抓，每次可以抓1个球或相连编号的2个球．甲先抓，规定谁抓到最后一次谁获胜．若甲第1次抓2023号球，最后甲获胜，则n=．
组卷：107引用：1难度：0.7 -
26．已知：如图，在Rt△ABC中，∠B=90°，AB=6cm,BC=8cm.点P从点A出发，沿AB方向匀速运动，速度为1cm/s；同时，点Q从点C出发，沿CA方向匀速运动，速度为2cm/s.过点Q作QD⊥AC，QD与BC相交于点D，连接PQ．设运动时间为t（s）
，解答下列问题：（0＜t≤165）
（1）当t为何值时，点A在线段PQ的垂直平分线上？
（2）在运动过程中，是否存在某一时刻t,使S△APQ：S四边形PBCQ=1：4？若存在，求出t的值；若不存在，请说明理由．
（3）当t为何值时，∠AQP=45°？
组卷：87引用：1难度：0.5
