2022-2023学年山东省济宁学院附中九年级（上）期中数学试卷（五四学制）

一、选择题（共12小题，每小题3分，共36分）

• 1．下列函数属于二次函数的是（　　）

  A．y=2（x-1）	B．y= 1 2 （x+1）2
  C．y=2（x+3）2-2x2	D．y=x+ 1 x
  组卷：145引用：5难度：0.9

  解析

• 2．下列抛物线中，与抛物线y=x²-2x+4具有相同对称轴的是（　　）

  A．y=4x2+2x+1

  B．y=2x2+4x+1

  C．y=x2-4x+2

  D．y=2x2-4x+1
  组卷：1040引用：2难度：0.5

  解析

• 3．二次函数y=（x+2）²-1的图象大致为（　　）

  A．

  B．

  C．

  D．
  组卷：5890引用：84难度：0.7

  解析

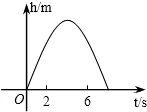• 4．竖直向上发射的小球的高度h（m）关于运动时间t（s）的函数表达式为h=at²+bt,其图象如图所示，若小球在发射后第2秒与第6秒时的高度相等，则下列时刻中小球的高度最高的是（　　）

  A．第3秒

  B．第3.5秒

  C．第4.2秒

  D．第6.5秒
  组卷：1292引用：19难度：0.9

  解析

• 5．在同一平面直角坐标系中，一次函数y=-kx+1与二次函数y=x²+k的大致图象可以是（　　）

  A．

  B．

  C．

  D．
  组卷：6971引用：33难度：0.6

  解析

• 6．二次函数y=ax²+4x+a的最大值为3，则a的值为（　　）

  A．-4

  B．-1

  C．1

  D．4
  组卷：275引用：5难度：0.6

  解析

• 7．若A（-

  3

  4

  ，y₁），B（-

  5

  4

  ，y₂），C（

  1

  4

  ，y₃）为二次函数y=x²+4x-5的图象上的三点，则y₁，y₂，y₃的大小关系是（　　）

  A．y1＜y2＜y3

  B．y2＜y1＜y3

  C．y3＜y1＜y2

  D．y1＜y3＜y2
  组卷：73引用：3难度：0.9

  解析

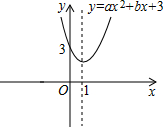• 8．如图，抛物线y=ax²+bx+3（a≠0）的对称轴为直线x=1，如果关于x的方程ax²+bx-6=0（a≠0）的一个根为4，那么该方程的另一个根为（　　）

  A．-2

  B．-1

  C．0

  D．3
  组卷：382引用：3难度：0.7

  解析

三、解答题（共4小题，共40分）

• 23．如图所示，隧道的截面由抛物线和矩形构成，矩形的长是12m,宽是4m.按照图中所示的直角坐标系，抛物线可以用y=-

  1

  6

  x²+bx+c表示，且抛物线上的点C到墙面OB的水平距离为3m,到地面OA的距离为

  1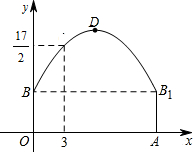7

  2

  m.
  
   （1）求该抛物线的函数关系式，并计算出拱顶D到地面OA的距离．
  （2）一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道，那么这辆货车能否安全通过？
  （3）在抛物线形拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米？
  组卷：295引用：3难度：0.6

  解析

• 24．已知△ABC是⊙O的内接三角形，∠BAC的平分线与⊙O相交于点D，连接DB．
  
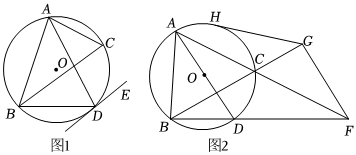
  （1）如图1，过点D作直线DE∥BC，求证：DE是⊙O的切线；
  （2）如图2，设弦BD，AC延长后交⊙O外一点F，过F作AD的平行线交BC的延长线于点G，过G作⊙O的切线GH（切点为H），求证：GF=GH．
  组卷：19引用：2难度：0.5

  解析