2023年黑龙江省齐齐哈尔市建华区中考数学三模试卷
发布：2024/9/7 5:0:8
一、单项选择题（每小题3分，满分30分）
-
1．实数-2023的相反数是（ ）
组卷：371引用：13难度：0.8 -
2．下面是一位美术爱好者利用网格图设计的几个英文字母的图形，你认为其中既是轴对称图形又是中心对称图形的是（ ）
组卷：75引用：41难度：0.9 -
3．下列计算正确的是（ ）
组卷：48引用：3难度：0.7 -
4．2023年，理化生实验操作将纳入中考．某校为提高学生的动手实验能力，特举行物理实验操作测试．共准备了三项不同的实验，要求每位学生只参加其中一项实验，由学生自己抽签确定做哪项实验．在这次测试中，小亮和小明恰好做同一项实验的概率是（ ）
组卷：121引用：3难度：0.5 -
5．甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数均是9.2环，方差依次为0.56、0.60、0.45、0.50，则成绩最稳定的是（ ）
组卷：61引用：1难度：0.5 -
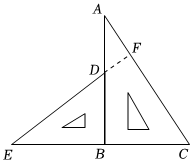6．把一副常用三角板按如图所示拼在一起，延长ED交AC于点F．那么∠AFE为（ ）组卷：217引用：1难度：0.9 -
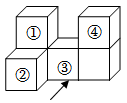7．如图，将六个小正方体按图示摆放，若移去一个有标号的小正方体，其主视图和俯视图都发生改变，这个小正方体的标号是（ ）组卷：232引用：5难度：0.8 -
8．为丰富学生的课余生活，王老师给小明50元钱，让他购买三种体育用品：大绳，小绳，毽子．其中大绳至多买两条，大绳每条14元，小绳每条5元，毽子每个2元，在把钱都用尽的条件下，小绳的买法共有（ ）
组卷：77引用：1难度：0.7
三、解答题（满分69分）
-
23．在综合实践课上，老师组织同学以“图形的旋转”为主题开展数学活动．下面是同学们进行相关问题的研究．
【观察猜想】如图①，△ACB和△EDB均为等边三角形，当点E、D分别在AB、CB边上，易证：AE=CD，∠ABC=60°；
【实践发现】如图②，将图①中的△EDB绕着点B逆时针旋转，连接AE、CD，线段AE与线段CD的数量关系为 ，直线AE与直线CD相交，所夹锐角为 °；
【类比探究】△ACB和△EDB均为直角三角形，∠ACB=∠EDB=90°．
（1）观察感知
如图③，当∠ABC=45°且点E、D分别在AB、CB边上，易证：AE=CD；2
（2）问题呈现
如图④，将图③中的△EDB绕着点B逆时针旋转，连接AE、CD．直线AE与直线CD交于点M．线段AE与线段CD的数量关系为 ，∠AMC=°；
（3）探究证明
如图⑤，当∠ABC=∠EBD=30°时，线段AE与线段CD的数量关系是什么？请说明理由．此时，∠AMC=°；
（4）拓展应用
在（3）的条件下，若BC=18，BD=12，将△EDB绕点B逆时针旋转一周，在整个旋转过程中，当点A、E、D三点共线时，请直接写出点C到直线AE的距离．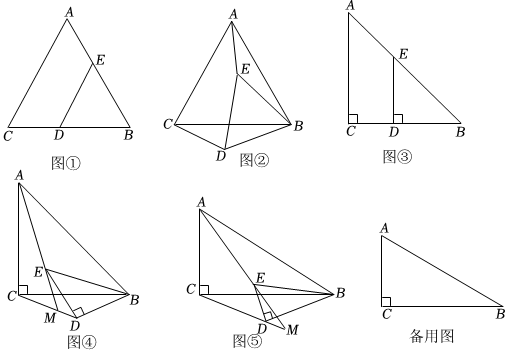
组卷：322引用：1难度：0.2 -
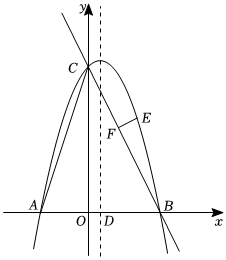24．如图，抛物线y=-+bx+c与x轴交于点A（-4，0）、点B，与y轴交于点C（0，12），连接AC．抛物线的对称轴与x轴交于点D，点E是直线BC上方抛物线上的一个动点（不与B、C重合），过点E作EF⊥BC交BC于点F．12x2
（1）求抛物线的解析式；
（2）点P是y轴上一动点，当CP+BP的和最小时，点P的坐标为 ；1010
（3）求四边形CDBE面积的最大值及此时E点的坐标；
（4）是否存在点E，使△CEF与△BOC相似，若存在请直接写出点E的坐标；若不存在，请说明理由．组卷：208引用：3难度：0.2
