当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省苏州市市区九年级（上）期中数学试卷

发布：2024/8/31 0:0:8

一、单选题（共10小题，每小题3分，满分30分）

1．用配方法解一元二次方程x²-4x-6=0时，配方后的方程是（　　）
A．（x+2）²=2 B．（x-2）²=2 C．（x+2）²=10 D．（x-2）²=10
组卷：2035引用：23难度：0.7
解析
2．为提高经济效益，某公司决定对一种电子产品进行降价促销．根据市场调查：这种电子产品销售单价定为200元时，每天可售出300个；若销售单价每降低2元，每天可多售出4个．已知每个电子产品的固定成本为100元，如果降价后公司每天获利30000元，那么这种电子产品降价后的销售单价为多少元？设这种电子产品降价后的销售单价为x元，则所列方程为（　　）
A．（x-100）[300+4（200-x）]=30000
B．（x-200）[300+2（100-x）]=30000
C．（x-100）[300+2（200-x）]=30000
D．（x-200）[300+4（100-x）]=30000
组卷：395引用：2难度：0.7
解析
3．已知二次函数y=-x²+6x-5，当1＜x＜4时，则函数值y的取值范围是（　　）
A．0＜y＜3 B．0＜y≤4 C．3＜y≤4 D．-5≤y≤4
组卷：1164引用：3难度：0.6
解析
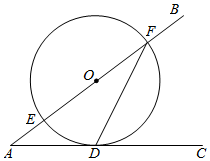4．如图，∠BAC=36°，点O在边AB上，⊙O与边AC相切于点D，交边AB于点E，F，连接FD，则∠AFD等于（　　）
A．27° B．29° C．35° D．37°
组卷：3308引用：34难度：0.6
解析
5．如图①，“东方之门”通过简单的几何曲线处理，将传统文化与现代建筑融为一体，最大程度地传承了苏州的历史文化．如图②，“门”的内侧曲线呈抛物线形，已知其底部宽度为80米，高度为200米．则离地面150米处的水平宽度（即CD的长）为（　　）
A．40米 B．30米 C．25米 D．20米
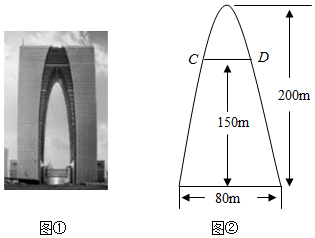组卷：690引用：4难度：0.6
解析
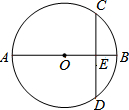6．如图，AB为⊙O的直径，CD为⊙O的弦，CD⊥AB，垂足为E，OE=3，CD=8，AB=（　　）
A．
2
7
B．10 C．
7
D．5
组卷：652引用：5难度：0.9
解析
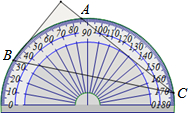7．将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B的读数分别为86°、30°，则∠ACB的大小为（　　）
A．15° B．28° C．29° D．34°
组卷：2226引用：164难度：0.9
解析
8．已知二次函数y=ax²+bx+c的图象与x轴交于点（-2，0）、（x₁，0）．且1＜x₁＜2，与y轴的负半轴相交．则下列关于a、b的大小关系正确的是（　　）
A．a＞0＞b B．a＞b＞0 C．b＞a＞0 D．b＜a＜0
组卷：1105引用：5难度：0.5
解析
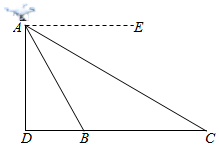9．如图，嘉琪在一座桥的附近试飞一架小型无人机，为了测量无人机飞行的高度AD，嘉琪通过操控装置测得无人机俯视桥头B，C的俯角分别为∠EAB=60°和∠EAC=30°，且D、B、C在同一水平线上．已知桥BC=30米，则无人机的飞行高度AD=（　　）
A．15米 B．15
3
米 C．（15
3
-15）米 D．（15
3
+15）米
组卷：1443引用：4难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共10小题，满分76分）

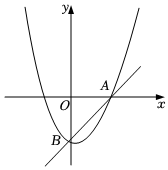27．在平面直角坐标系中，一次函数y=x-2的图象与x轴交于点A，与y轴交于点B，二次函数的图象y=ax²+bx+c（a＞0）经过点A、B．
（1）求a、b满足的关系式及c的值；
（2）如果a=1，点P是直线AB下方抛物线上的一点，过点P作PD垂直于x轴，垂足为点D，交直线AB于点E，使DE=PE．
①求点P的坐标；
②直线PD上是否存在点Q，使△ABQ为直角三角形？若存在，求出符合条件的所有点Q的坐标；若不存在，请说明理由．
组卷：395引用：5难度：0.3
解析
28．如图1，直线l：y=-
4
3
x+4与x轴、y轴分别交于A、B两点，二次函数y=ax²-2ax-2（a＞0）的图象经过点A，交y轴于点C．
（1）则点C坐标为
；抛物线对称轴是
；a的值是
；
（2）已知点M是抛物线上的一个动点，经过点M作x轴的垂线MD，交直线l于点E，过点C作CD⊥MD，垂足为D，连接CM．设点M的横坐标为m.
①当点M位于第一象限的抛物线上，且△CDM是等腰直角三角形时，CM交直线l于点F，设点F至直线DM的距离d₁，到y轴的距离为d₂，求
d
1
d
2
的值．
②如图2，将△CDM绕点C逆时针旋转得至△CD′M′，且旋转角∠MCM′=∠OAB，当点M的对应点M′落在y轴上时，请直接写出点M的横坐标m的值．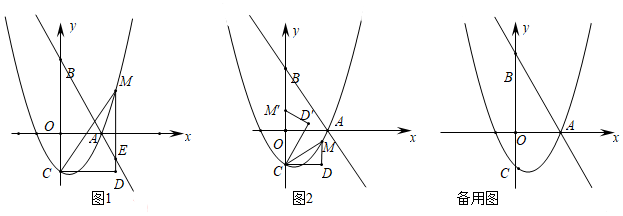
组卷：708引用：3难度：0.2
解析