2022-2023学年湖北省襄阳市襄城区八年级（下）期末数学试卷

一、选择题（本大题共10个小题，每小题3分，共30分）在每小题给出的四个选项中，只有一项是符合题目要求的，请将其序号在答题卡上涂黑作答.

• 1．化简

  20

  的结果是（　　）

  A．2 10

  B．2 5

  C．4 5

  D．10 2
  组卷：317引用：6难度：0.8

  解析

• 2．下列各组数据中能作为直角三角形的三边长的是（　　）

  A．1，2，2

  B．1，1， 3

  C．4，5，6

  D．1， 3 ，2
  组卷：855引用：22难度：0.9

  解析

• 3．甲乙两名同学本学期参加了相同的5次数学考试，老师想判断这两位同学的数学成绩谁更稳定，老师需比较这两人5次数学成绩的（　　）

  A．平均数

  B．中位数

  C．众数

  D．方差
  组卷：807引用：14难度：0.9

  解析

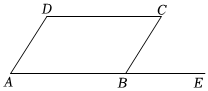• 4．如图，四边形ABCD是平行四边形，∠CBE=45°，则∠D的度数为（　　）

  A．150°

  B．135°

  C．120°

  D．105°
  组卷：10引用：1难度：0.5

  解析

• 5．使

  x

  -

  2

  有意义的x的取值范围在数轴上表示为（　　）

  A．	B．
  C．	D．
  组卷：522引用：10难度：0.7

  解析

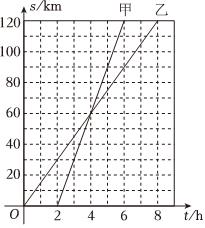• 6．若A，B两地相距120km,甲和乙沿相同的路线由A地到B地，行驶路程s与时间t的关系如图所示．根据图象信息判断以下结论不正确的是（　　）

  A．甲比乙早两小时到达B地

  B．当乙行驶5h时，甲比乙多走15km

  C．乙出发4h后，甲在乙的前面

  D．甲行驶的路程s与时间t的函数关系是 s=30t
  组卷：28引用：1难度：0.5

  解析

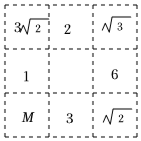• 7．在如图的方格中，若要使横，竖，斜对角的3个实数相乘都得到同样的结果，则空格中M代表的实数为（　　）

  A． 6 2

  B． 2 3

  C． 6

  D． 6 6
  组卷：235引用：5难度：0.6

  解析

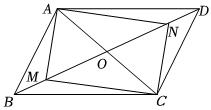• 8．如图，在平行四边形ABCD中，M、N是BD上两点，BM=DN，连接AM、MC、CN、NA，添加一个条件，使四边形AMCN是矩形，这个条件是（　　）

  A．MB=MO

  B．OM= 1 2 AC

  C．BD⊥AC

  D．∠AMB=∠CND
  组卷：2949引用：29难度：0.5

  解析

三、解答题（本大题共9个小题，共72分）解答应写出文字说明、证明过程或演算步骤.

• 24．（1）观察发现：如图1，已知Rt△ABC，∠ABC=90°，分别以AB，BC为边，向外作正方形ABDE和正方形BCFG，连接DG．若M是DG的中点，不难发现：BM=

  1

  2

  AC．
  请完善下面证明思路：①先根据

  ，证明BM=

  1

  2

  DG；②再证明

  ，得到DG=AC；所以BM=

  1

  2

  AC；
  （2）数学思考：若将上题的条件改为：“已知Rt△ABC，∠ABC=90°，分别以AB，AC为边向外作正方形ABDE和正方形ACHI，N是EI的中点”，则相应的结论“AN=

  1

  2

  BC”成立吗？
  小颖通过添加如图2所示的辅助线验证了结论的正确性．请写出小颖所添加的辅助线的作法，并由此证明该结论；
  （3）拓展延伸：如图3，已知等腰△ABC和等腰△ADE，AB=AC，AD=AE．连接BE，CD，若P是CD的中点，探索：当∠BAC与∠DAE满足什么条件时，AP=

  1

  2

  BE，并简要说明证明思路．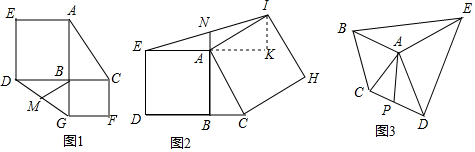
  
  组卷：230引用：2难度：0.3

  解析

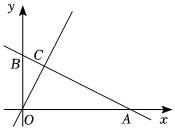• 25．如图，在平面直角坐标系中，直线 y=kx+b（k≠0）与x轴，y轴分别相交于A，B两点，OA=5，

  OB

  =

  5

  2

  ，直线y=2x与直线AB交于点C．
  （1）求直线AB的解析式；
  （2）判断△OAC的形状，并说明理由；
  （3）动点P在直线AB上，动点Q在直线OC上，当以O，B，P，Q为顶点的四边形是平行四边形时，求P，Q两点的坐标．
  组卷：144引用：1难度：0.3

  解析