2022-2023学年广东省深圳市南山区九年级（下）期末数学模拟测试试卷

一．选择题（共10小题，满分0分）

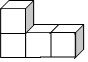• 1．如图，是由四个完全相同的小正方形组合而成的几何体，从上面看它得到的平面图形是（　　）

  A．

  B．

  C．

  D．
  组卷：149引用：3难度：0.9

  解析

• 2．下列各数中，可以用来证明命题“任何偶数都是8的整数倍”是假命题的反例是（　　）

  A．32

  B．16

  C．8

  D．4
  组卷：152引用：20难度：0.9

  解析

• 3．黑色不透明口袋里装有红色、白色球共10个，它们除颜色外都相同．从口袋中随机摸出一个球，记下颜色后放回，并摇匀，不断重复上述实验1000次，其中200次摸到红球，则可估计口袋中红色球的个数是（　　）

  A．2

  B．4

  C．6

  D．8
  组卷：483引用：5难度：0.7

  解析

• 4．一元二次方程x²-ax+1=0的两实数根相等，则a的值为（　　）

  A．a=0

  B．a=2或a=-2

  C．a=2

  D．a=2或a=0
  组卷：402引用：8难度：0.9

  解析

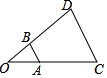• 5．如图，以点O为位似中心，将△OAB放大后得到△OCD，OA=2，AC=3，则△OAB与△OCD的面积比为（　　）

  A．2：3

  B．2：5

  C．4：9

  D．4：25
  组卷：248引用：6难度：0.7

  解析

• 6．关于反比例函数y=

  6

  x

  ，下列说法错误的是（　　）

  A．图象经过点（2，3）

  B．图象分布在第二、四象限

  C．图象关于原点对称

  D．图象与坐标轴没有交点
  组卷：554引用：3难度：0.7

  解析

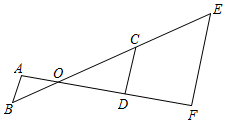• 7．如图AB∥CD∥EF，AF、BE相交于O，若AO=OD=DF=3cm,BE=10cm,则BO的长为（　　）

  A． 10 3 cm

  B．5cm

  C． 5 2 cm

  D．3cm
  组卷：999引用：3难度：0.8

  解析

三．解答题（共7小题，满分0分）

• 21．（1）问题发现：
  如图1，在正方形ABCD中，点E，F，G，H分别在边AB，CD，AD，BC上，且EF⊥GH，则

  EF

  GH

  =

  ；
  （2）类比探究：
  如图2，在（1）的条件下，把“正方形ABCD”改为“矩形ABCD，且AB=m,BC=n”其它条件不变，则

  EF

  GH

  =

  ，证明你的结论；
  （3）拓展应用：
  如图3，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，点D为AC的中点，连接BD，点E为AB上一点，CE⊥BD，则CE=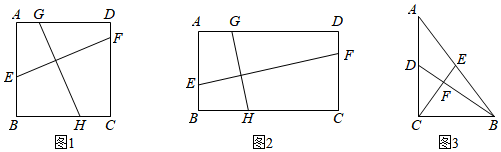

  ．
  
  组卷：1026引用：6难度：0.3

  解析

• 22．如图1，已知在平面直角坐标系xOy中，四边形OABC是矩形，点A，C分别在x轴和y轴的正半轴上，连结AC，OA=3，∠OAC=30°，点D是BC的中点，
  
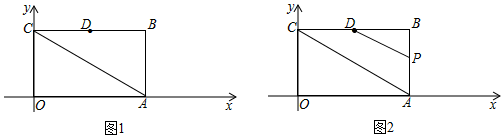
  （1）OC=

  ；点D的坐标为

  ；
  （2）若点E在线段OA上，直线DE把矩形OABC面积分成为2：1两部分，求点E坐标；
  （3）如图2．点P为线段AB上一动点（含线段端点），连接DP；以线段DP为边，在DP所在直线的右上方作等边△DPQ，当动点P从点B运动到点A时，点Q也随之运动，当△ACQ成为以AC为底的等腰三角形时，直接写出Q点的横坐标．
  组卷：223引用：3难度：0.3

  解析