2022-2023学年天津市东丽区九年级（上）期末数学试卷

一、选择题（本大题共12小题，每小题3分，共36分）

• 1．如图图形中既是中心对称图形又是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：181引用：3难度：0.8

  解析

• 2．下列方程是一元二次方程的是（　　）

  A．x2-2x+ 1 x =0

  B．y=2x2-3x-1

  C．x2-1=0

  D．y2-x+3=0
  组卷：418引用：7难度：0.8

  解析

• 3．将抛物线y=2x²向左平移3个单位，所得抛物线的解析式是（　　）

  A．y=2（x+3）2

  B．y=2（x-3）2

  C．y=2x2+3

  D．y=2x2-3
  组卷：224引用：6难度：0.6

  解析

• 4．下列事件是随机事件的是（　　）

  A．标准大气压下，通常加热到100℃，水会沸腾

  B．明天太阳从东方升起

  C．随意翻到一本书的某页，这页的页码是偶数

  D．从装有黑球、白球的袋里摸出绿球
  组卷：217引用：3难度：0.9

  解析

• 5．若⊙O的半径为5cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是（　　）

  A．点A在圆外

  B．点A在圆上

  C．点A在圆内

  D．不能确定
  组卷：1396引用：74难度：0.9

  解析

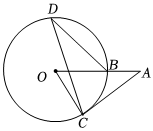• 6．如图，OA交⊙O于点B，AC切⊙O于点C，D点在⊙O上，若∠D=26°，则∠A为（　　）

  A．38°

  B．30°

  C．64°

  D．52°
  组卷：571引用：3难度：0.5

  解析

• 7．如图，在Rt△ABC中，∠B=90°，BC=3，AB=4，将△ABC绕点A顺时针旋转90°得到△AB'C'，连接CC'，则CC'的长为（　　）

  A．5

  B． 5 2

  C． 2 5

  D． 10
  组卷：627引用：5难度：0.7

  解析

• 8．二次函数y=2x²-8x+m的图象与x轴有两个交点，若其中一个交点的坐标为（-1，0），则另一个交点坐标为（　　）

  A．（-3，0）

  B．（3，0）

  C．（5，0）

  D．（9，0）
  组卷：1127引用：2难度：0.6

  解析

三、解答题（本大题共7小题，共66分，解答应写出文字说明、演算步骤或推理过程）

• 24．（1）特殊情景：如图（1），在四边形ABCD中，AB=AD，以点A为顶点作一个角，角的两边分别交BC，CD于点E，F，且∠EAF=

  1

  2

  ∠BAD，连接EF，若∠BAD=∠B=∠D=90°，探究：线段BE，DF，EF之间的数量关系，并说明理由．
  （2）类比猜想：类比特殊情景，在上述（1）条件下，把“∠BAD=∠B=∠D=90°”改成一般情况“∠B+∠D=180°，”如图（2），小明猜想：设∠BAD=α，线段BE，DF，EF之间的数量关系是否仍然成立？若成立，请你写出结论；若不成立，请你写出成立时α的取值范围．
  （3）解决问题：如图（3），在△ABC中，∠BAC=90°，AB=AC=4，点D，E均在边BC上，且∠DAE=45°，若BD=

  2

  ，计算DE的长度．
  
  组卷：512引用：5难度：0.3

  解析

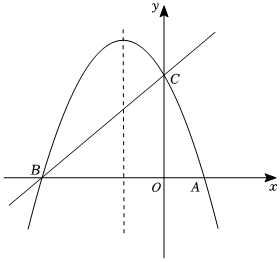• 25．如图，已知抛物线y=-x²+bx+c经过B（-3，0），C（0，3）两点，与x轴的另一个交点为A．
  （1）求抛物线的解析式；
  （2）若直线y=mx+n经过B，C两点，则m=

  ；n=

  ；
  （3）在抛物线对称轴上找一点E，使得AE+CE的值最小，直接写出点E的坐标；
  （4）设点P为x轴上的一个动点，是否存在使△BPC为等腰三角形的点P，若存在，直接写出点P的坐标；若不存在，说明理由．
  组卷：1177引用：4难度：0.1

  解析