2023-2024学年湖北省武汉市洪山区英格教育集团八年级（上）月考数学试卷（10月份）
发布：2024/9/17 3:0:8
一、选择题（共10小题，每小题3分，共30分）
-
1．下列每组数分别是三根小木棒的长度，用它们能摆成三角形的是（ ）
组卷：5384引用：110难度：0.9 -
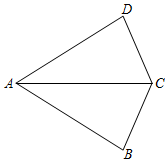2．如图，∠DAC=∠BAC，下列条件中，不能判定△ABC≌△ADC的是（ ）组卷：742引用：10难度：0.7 -
3．一个三角形的三个内角度数之比为4：5：9，则这个三角形是（ ）
组卷：488引用：18难度：0.8 -
4．已知正多边形的一个内角为144°，则该正多边形的边数为（ ）
组卷：1728引用：12难度：0.9 -
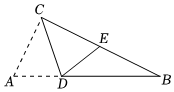5．如图，在△ABC中，∠ACB=90°，点D在AB上，沿CD折叠，使A点落在BC边上的E点，若∠B=26°，则∠CDE的度数为（ ）组卷：1225引用：9难度：0.7 -
6．下列说法错误的有（ ）个．
①三角形的高不在三角形内就在三角形外；
②多边形的内角和必小于它的外角和；
③周长和面积相等的两个三角形全等；
④周长相等的两个等边三角形全等；
⑤两边和一角分别对应相等的两个三角形全等；
⑥等腰三角形顶角的外角平分线平行于这个等腰三角形的底．组卷：27引用：1难度：0.8 -
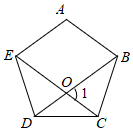7．如图，EC，BD是正五边形ABCDE的对角线，则∠1的大小为（ ）组卷：489引用：3难度：0.6 -
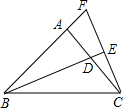8．等腰Rt△ABC中，∠BAC=90°，D是AC的中点，EC⊥BD于E，交BA的延长线于F，若BF=12，则△FBC的面积为（ ）组卷：3841引用：28难度：0.5
三、解答题（共8题，共72分）
-
23．△ABC和△ADE共顶点A（∠BAE＜180°），AB=AC，AD=AE．
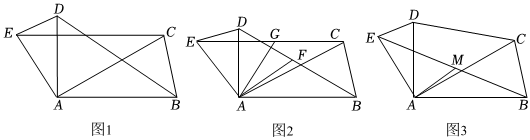
（1）【问题背景】如图1，∠BAC=∠DAE，求证：BD=CE；
（2）【探究运用】如图2，∠BAC=∠DAE=α，F，G分别为BD，CE的中点，连接AG，AF，求∠GAF的度数（用含α的式子表示）；
（3）【创新拓展】如图3，连接BE，若M为BE的中点，且∠DAC=∠ABE+∠AEB，求证：DC=2AM．组卷：204引用：2难度：0.3 -
24．已知：在平面直角坐标系中，放入一块等腰直角三角板ABC，∠BAC=90°，AB=AC，A点的坐标为（0，a），B点的坐标为（b,0）．且a,b满足b=
a-2+4，D的坐标为（-2.1，0）．+2-a
（1）如图1，求C点的坐标；
（2）在前面的条件下作等腰Rt△ADE，使AD=EA，∠EAD=90°，D点刚好落在x轴的负半轴，连CE交y轴于M．如图2，
①求证ME=MC，
②求△AEC的面积；
（3）在（2）的条件下，若N的坐标是（-4，-2），P在第二象限，且P，N，M构成的三角形是等腰直角三角形，则P点坐标为．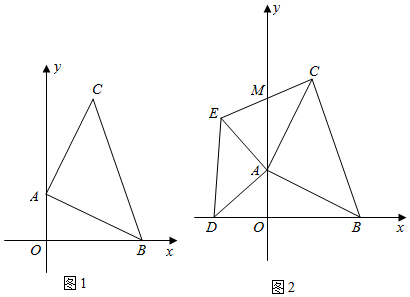
组卷：260引用：2难度：0.2
