2022-2023学年宁夏银川一中高二（下）期末数学试卷（理科）

一、单选题（本题共12小题，每小题5分，共60分）

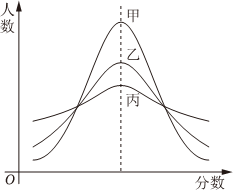• 1．某市期末教学质量检测，甲、乙、丙三科考试成绩近似服从正态分布，则由如图曲线可得下列说法中正确的是（　　）

  A．甲学科总体的均值最小

  B．乙学科总体的方差及均值都居中

  C．丙学科总体的方差最大

  D．甲、乙、丙的总体的均值不相同
  组卷：40引用：1难度：0.7

  解析

• 2．若直线的参数方程为

  x = - 1 + tsin 40 °

  y = 3 + tcos 40 °

  （t为参数），则其倾斜角为（　　）

  A．40°

  B．50°

  C．140°

  D．130°
  组卷：53引用：3难度：0.7

  解析

• 3．设x∈R，则“

  x

  -

  5

  2

  -

  x

  ＞

  0

  ”是“|x-1|＜4”的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：412引用：8难度：0.8

  解析

• 4．在极坐标系中，把曲线C：ρ=2sinθ绕极点逆时针旋转

  π

  6

  后所得曲线的方程为（　　）

  A． ρ = 2 sin （ θ + π 6 ）	B． ρ = 2 sin （ θ - π 6 ）
  C． ρ = 2 cos （ θ + π 6 ）	D． ρ = 2 cos （ θ - π 6 ）
  组卷：37引用：3难度：0.5

  解析

• 5．已知某批零件的长度误差（单位：毫米）服从正态分布N（0，3²），从中随机取一件，其长度误差落在区间（3，6）内的概率为（　　）
  （附：若随机变量ξ服从正态分布N（μ，σ²），则P（μ-σ≤ξ≤μ+σ）≈68.27%，P（μ-2σ≤ξ≤μ+2σ）≈95.45%）

  A．4.56%

  B．13.59%

  C．27.18%

  D．31.74%
  组卷：182引用：2难度：0.8

  解析

• 6．有下列说法：
  ①若某商品的销售量5（件）关于销售价格x（元/件）的线性回归方程为y

  ̂

  y

  =

  -

  5

  x

  +

  350

  ，当销售价格为10元时，销售量一定为300件；
  ②线性回归直线：

  ̂

  y

  =

  ̂

  b

  x

  +

  ̂

  a

  一定过样本点中心（

  x

  ,

  y

  ）；
  ③若两个随机变量的线性相关性越强，则相关系数r的值越接近于1；
  ④在残差图中，残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适，与带状区域的宽度无关；
  ⑤在线性回归模型中，相关指数R²表示解释变量对于预报变量变化的贡献率，R²越接近于1，表示回归的效果越好；
  其中正确的结论有几个（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：222引用：4难度：0.7

  解析

• 7．若

  P

  （

  AB

  ）

  =

  1

  9

  ，

  P

  （

  A

  ）

  =

  2

  3

  ，

  P

  （

  B

  ）

  =

  1

  3

  ，则事件A与B的关系是（　　）

  A．互斥但不对立	B．对立
  C．相互独立	D．既互斥又独立
  组卷：386引用：5难度：0.5

  解析

三、解答题：（共70分．解答应写出文字说明、证明过程或演算步骤．）

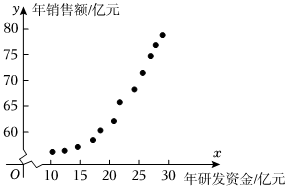• 21．多年来，清华大学电子工程系黄翊东教授团队致力于光谱成像芯片的研究，2022年6月研制出国际首款实时超光谱成像芯片，相比已有光谱检测技术，实现了从单点光谱仪到超光谱成像芯片的跨越为制定下一年的研发投入计划，该研发团队为需要了解年研发资金投入量x（单位：亿元）对年销售额y（单位：亿元）的影响，结合近12年的年研发资金投入量x_i和年销售额y_i的数据（i=1，2，…12），该团队建立了两个函数模型：①y=α+βx²，②y=e^λx+t，其中α，β，λ，t均为常数，e为自然对数的底数．经对历史数据的初步处理，得到右侧散点图如图．
  令

  u

  i

  =

  x

  2

  i

  ，v_i=lny_i（i=1，2，…，12），计算得如下数据：
  

  x	y	12 ∑ i = 1 （xi- x ）2	12 ∑ i = 1 （yi- y ）2	12 ∑ i = 1 （xi- x ）（vi- v ）
  20	66	770	200	14
  u	v	12 ∑ i = 1 （ui- u ）2	12 ∑ i = 1 （vi- v ）2	12 ∑ i = 1 （u1- u ）（yi- y ）
  460	4.20	3125000	0.308	21500

  （1）设{u_i}和{y_i}的相关系数为r₁，{x_i}和{v_i}的相关系数为r₂，请从相关系数的角度，选择一个拟合程度更好的模型；
  （2）（i）根据（1）的选择及表中数据，建立y关于x的回归方程（系数精确到0.01）；
  （ii）若下一年销售额y需达到80亿元，预测下一年的研发资金投入量x是多少亿元？
  附：①相关系数

  ̂

  r

  =

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  （

  y

  i

  -

  y

  ）

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  n

  ∑

  i

  =

  1

  （

  y

  i

  -

  y

  ）

  2

  ，回归直线

  ̂

  y

  =

  a

  +

  bx

  中斜率和截距的最小二乘估计公式分别为：

  ̂

  b

  =

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  （

  y

  i

  -

  y

  ）

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  ，

  ̂

  a

  =

  y

  -

  ̂

  b

  x

  ；
  ②参考数据：308=77×4，

  80

  ≈8.9443，e^4.3820≈80．
  组卷：803引用：4难度：0.5

  解析

• 22．中国提出共建“一带一路”，旨在促进更多的经济增长和更大的互联互通，随着“一带一路”的发展，中亚面粉、波兰苹果、法国红酒走上了国人的餐桌，中国制造的汽车、电子元件、农产品丰富着海外市场．为拓展海外市场，某电子公司新开发一款电子产品，该电子产品的一个系统G有3个电子元件组成，各个电子元件能正常工作的概率为

  2

  3

  ，且每个电子元件能否正常工作相互独立，若系统G中有超过一半的电子元件正常工作，则G可以正常工作，否则就需要维修，且维修所需费用为900元．
  （1）求系统需要维修的概率；
  （2）该电子产品共由3个系统G组成，设ξ为电子产品所需要维修的费用，求ξ的期望；
  （3）为提高系统G正常工作的概率，在系统内增加两个功能完全一样的其他品牌的电子元件，每个新元件正常工作的概率为p,且新增元件后有超过一半的电子元件正常工作，则G可以正常工作．问：p满足什么条件时可以提高整个系统G的正常工作概率？
  组卷：220引用：3难度：0.4

  解析