人教新版八年级上册《11.2 与三角形有关的角》2023年同步练习卷（6）

一、选择题

• 1．一个三角形三个内角的度数之比为4：5：6，这个三角形一定是（　　）

  A．直角三角形

  B．等腰三角形

  C．锐角三角形

  D．钝角三角形
  组卷：1076引用：10难度：0.6

  解析

• 2．在△ABC中，2（∠A+∠B）=3∠C，则∠C的补角等于（　　）

  A．36°

  B．72°

  C．108°

  D．144°
  组卷：1974引用：9难度：0.5

  解析

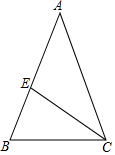• 3．如图，CE是△ABC的角平分线，若∠B=∠ACB，∠BAC=40°，则∠ACE的度数是（　　）

  A．20°

  B．35°

  C．40°

  D．70°
  组卷：47引用：3难度：0.6

  解析

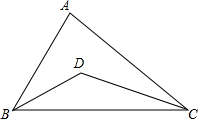• 4．如图，在△ABC中，点D是∠ABC和∠ACB的角平分线的交点，∠A=80°，∠ABD=30°，则∠DCB为（　　）

  A．25°

  B．20°

  C．15°

  D．10°
  组卷：1176引用：8难度：0.5

  解析

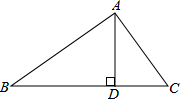• 5．如图，三角形ABC，∠BAC=90°，AD是三角形ABC的高，图中相等的是（　　）

  A．∠B=∠C

  B．∠BAD=∠B

  C．∠C=∠BAD

  D．∠DAC=∠C
  组卷：868引用：10难度：0.8

  解析

• 6．图中，∠2的度数是（　　）
  

  A．110°

  B．70°

  C．60°

  D．40°
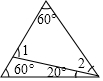  组卷：498引用：5难度：0.7

  解析

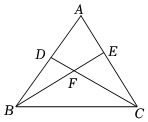• 7．如图，D是AB上一点，E是AC上一点，BE，CD相交于点F，∠A=60°，∠ACD=35°，∠ABE=20°，则∠BFD为（　　）

  A．95°

  B．115°

  C．75°

  D．65°
  组卷：272引用：3难度：0.7

  解析

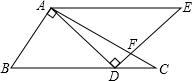• 8．如图，将一副三角板如图放置，若AE∥BC，则∠BAD=（　　）

  A．90°

  B．85°

  C．75°

  D．65°
  组卷：814引用：8难度：0.5

  解析

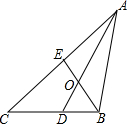• 9．如图，在△ABC中，AD和BE是角平分线，其交点为O，若∠BOD=70°，则∠ACB的度数为（　　）

  A．10°

  B．20°

  C．30°

  D．40°
  组卷：765引用：5难度：0.6

  解析

• 10．在下列条件中，不能确定△ABC是直角三角形的条件是（　　）

  A．∠A= 1 2 ∠B= 1 3 ∠C	B．∠A=2∠B=3∠C
  C．∠A=∠B= 1 2 ∠C	D．∠A=2∠B=2∠C
  组卷：652引用：5难度：0.5

  解析

三、解答题

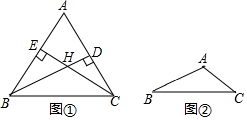• 29．（1）如图①，△ABC是锐角三角形，高BD、CE相交于点H，找出∠BHC和∠A之间存在何种等量关系；
  （2）如图②，若△ABC是钝角三角形，∠A＞90°，高BD、CE所在的直线相交于点H，把图②补充完整，并指出此时（1）中的等量关系是否仍然成立？
  组卷：214引用：4难度：0.3

  解析

• 30．问题情景：如图1，△ABC中，有一块直角三角板PMN放置在△ABC上（P点在△ABC内），使三角板PMN的两条直角边PM、PN恰好分别经过点B和点C，试问∠ABP与∠ACP是否存在某种确定的数量关系？
  
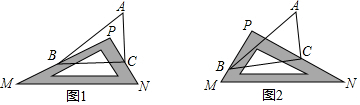
  （1）特殊探究：若∠A=40°，则∠ABC+∠ACB=

  度，∠PBC+∠PCB=

  度，∠ABP+∠ACP=

  度．
  （2）类比探索：请探究∠ABP+∠ACP与∠A的关系；
  （3）类比延伸：如图2，改变直角三角板PMN的位置：使P点在△ABC外，三角板PMN的两条直角边PM、PN仍然分别经过点B和点C，（2）中的结论是否仍然成立？若不成立，请直接写出你的结论．
  组卷：734引用：4难度：0.5

  解析