当前位置：试卷中心 > 试卷详情

2023-2024学年重庆市巴南区科学城中学九年级（上）开学数学试卷

发布：2024/7/23 8:0:8

一、单选题（每小题4分，共40分）

1．下列新能源汽车标志图案中，既是轴对称图形，又是中心对称图形的是（　　）
A． B． C． D．
组卷：71引用：4难度：0.9
解析
2．要从
y
=
4
3
x
的图象得到直线
y
=
4
x
+
2
3
，就要将直线
y
=
4
3
x
（　　）
A．向上平移
2
3
个单位 B．向下平移
2
3
个单位
C．向上平移2个单位 D．向下平移2个单位
组卷：598引用：9难度：0.9
解析
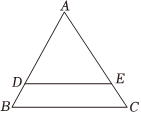3．如图，在△ABC中，D是AB边上一点，过点D作DE∥BC交AC于点E，若AD：DB=3：1，则S_△ADE：S_△ABC的值为（　　）
A．
3
7
B．
3
4
C．
16
9
D．
9
16
组卷：456引用：4难度：0.5
解析
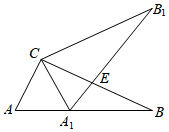4．如图，在△ABC中，∠ACB=90°，将△ABC绕点C逆时针旋转得到△A₁B₁C，此时使点A的对应点A₁恰好在AB边上，点B的对应点为B₁，A₁B₁与BC交于点E，则下列结论一定正确的是（　　）
A．AB=EB₁ B．CA₁=A₁B
C．A₁B₁⊥BC D．∠CA₁A=∠CA₁B₁
组卷：494引用：5难度：0.7
解析
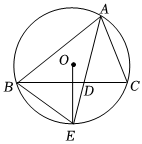5．如图，△ABC内接于⊙O，E是
ˆ
BC
的中点，连接BE，OE，AE，若∠BAC=70°，则∠OEB的度数为（　　）
A．70° B．65° C．60° D．55°
组卷：989引用：6难度：0.5
解析
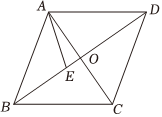6．如图，在菱形ABCD中，对角线AC与BD交于点O，在BD上取一点E，使得AE=BE，AB=10，AC=12，则BE长为（　　）
A．
25
4
B．
25
2
C．
25
3
D．
21
4
组卷：542引用：4难度：0.6
解析
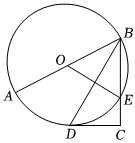7．如图，AB是⊙O的直径，E为⊙O上一点，BD垂直平分OE交⊙O于点D，过点D的切线与BE的延长线交于点C．若
CD
=
3
，则AB的长为（　　）
A．4 B．2 C．
4
3
D．
2
3
组卷：621引用：4难度：0.5
解析
8．如图，在同一平面直角坐标系中，二次函数y=ax²+bx+c（a≠0）与一次函数y=acx+b的图象可能是（　　）
A． B． C． D．
组卷：1843引用：10难度：0.5
解析
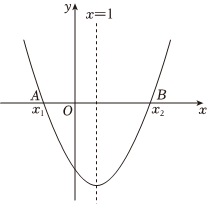9．如图，二次函数y=ax²+bx+c的图象关于直线x=1对称，与x轴交于A（x₁，0），B（x₂，0）两点，若-2＜x₁＜-1，则下列四个结论：①3＜x₂＜4，②3a+2b＞0，③b²＞a+c+4ac,④a＞b＞c,⑤a（m+1）（m-1）＜b（1-m）．正确结论的个数为（　　）
A．1个 B．2个 C．3个 D．4个
组卷：455引用：5难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共86分）

26．如图，抛物线y=ax²+bx+c与x轴交于A，B两点，点B的坐标为
（
2
，
0
）
，抛物线与y轴交于点C（0，-2
2
），对称轴为直线
x
=
-
3
2
2
，连接AC，过点B作BE∥AC交抛物线于点E．
（1）求抛物线的解析式；
（2）点P是线段AC下方抛物线上的一个动点，过点P作PF∥y轴交直线BE于点F，过点F作FD⊥AC交直线AC于点D，连接PD，求△FDP面积的最大值及此时点P的坐标；
（3）在第（2）小问的条件下，将原抛物线沿着射线CB方向平移，平移后的抛物线过点B，点M在平移后抛物线的对称轴上，点T是平面内任意一点，是否存在以B、P、M、T为顶点的四边形是以BP为边的菱形，若存在，直接写出点T的坐标，若不存在，请说明理由．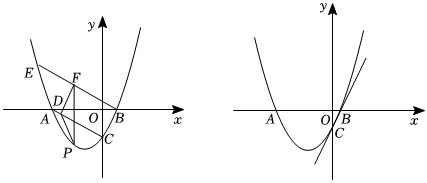
组卷：383引用：2难度：0.2
解析
27．如图，已知△ABC为等腰直角三角形，AC=BC且∠ACB=90°，D为AB上一动点，连接CD，把CD绕点D旋转90°得到ED，连接CE；
（1）如图1，CE交AB于点Q，若
BC
=
6
2
，DQ=5，求AQ的长；
（2）如图2，连接BE、AE，点F为BE中点，求证：AE=2DF；
（3）如图3，连接BE，以BE为斜边在BE右侧作以点H为直角顶点的等腰Rt△HEB，点Q为BC上一点且CQ=3BQ，点N为AB上一动点，把△BQN沿着QN翻折到△BQN的同一平面得△MQN，连接HM，若AC=4，当HM取最小值时，请直接写出S_△HMN的值．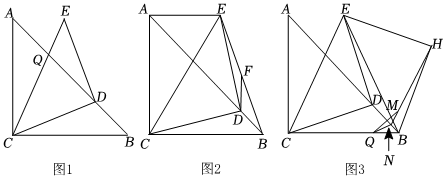
组卷：553引用：4难度：0.1
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．向上平移 2 3 个单位	B．向下平移 2 3 个单位
C．向上平移2个单位	D．向下平移2个单位

A．AB=EB₁	B．CA₁=A₁B
C．A₁B₁⊥BC	D．∠CA₁A=∠CA₁B₁

2023-2024学年重庆市巴南区科学城中学九年级（上）开学数学试卷

一、单选题（每小题4分，共40分）

1．下列新能源汽车标志图案中，既是轴对称图形，又是中心对称图形的是（ ）

2．要从y=43x的图象得到直线y=4x+23，就要将直线y=43x（ ）

3．如图，在△ABC中，D是AB边上一点，过点D作DE∥BC交AC于点E，若AD：DB=3：1，则S△ADE：S△ABC的值为（ ）

4．如图，在△ABC中，∠ACB=90°，将△ABC绕点C逆时针旋转得到△A1B1C，此时使点A的对应点A1恰好在AB边上，点B的对应点为B1，A1B1与BC交于点E，则下列结论一定正确的是（ ）

5．如图，△ABC内接于⊙O，E是ˆBC的中点，连接BE，OE，AE，若∠BAC=70°，则∠OEB的度数为（ ）

6．如图，在菱形ABCD中，对角线AC与BD交于点O，在BD上取一点E，使得AE=BE，AB=10，AC=12，则BE长为（ ）

7．如图，AB是⊙O的直径，E为⊙O上一点，BD垂直平分OE交⊙O于点D，过点D的切线与BE的延长线交于点C．若CD=3，则AB的长为（ ）

8．如图，在同一平面直角坐标系中，二次函数y=ax2+bx+c（a≠0）与一次函数y=acx+b的图象可能是（ ）

9．如图，二次函数y=ax2+bx+c的图象关于直线x=1对称，与x轴交于A（x1，0），B（x2，0）两点，若-2＜x1＜-1，则下列四个结论：①3＜x2＜4，②3a+2b＞0，③b2＞a+c+4ac,④a＞b＞c,⑤a（m+1）（m-1）＜b（1-m）．正确结论的个数为（ ）

三、解答题（共86分）

1．下列新能源汽车标志图案中，既是轴对称图形，又是中心对称图形的是（　　）

2．要从
y
=
4
3
x
的图象得到直线
y
=
4
x
+
2
3
，就要将直线
y
=
4
3
x
（　　）

3．如图，在△ABC中，D是AB边上一点，过点D作DE∥BC交AC于点E，若AD：DB=3：1，则S_△ADE：S_△ABC的值为（　　）

4．如图，在△ABC中，∠ACB=90°，将△ABC绕点C逆时针旋转得到△A₁B₁C，此时使点A的对应点A₁恰好在AB边上，点B的对应点为B₁，A₁B₁与BC交于点E，则下列结论一定正确的是（　　）

5．如图，△ABC内接于⊙O，E是
ˆ
BC
的中点，连接BE，OE，AE，若∠BAC=70°，则∠OEB的度数为（　　）

6．如图，在菱形ABCD中，对角线AC与BD交于点O，在BD上取一点E，使得AE=BE，AB=10，AC=12，则BE长为（　　）

7．如图，AB是⊙O的直径，E为⊙O上一点，BD垂直平分OE交⊙O于点D，过点D的切线与BE的延长线交于点C．若
CD
=
3
，则AB的长为（　　）

8．如图，在同一平面直角坐标系中，二次函数y=ax²+bx+c（a≠0）与一次函数y=acx+b的图象可能是（　　）