2023年湖北省襄阳市老河口市中考数学适应性试卷
发布:2024/8/16 2:0:0
一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将其标号在答题卡上涂黑作答.
-
1.下列实数中,是有理数的是( )
组卷:89引用:1难度:0.8 -
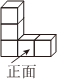 2.如图是由5个相同的小正方体组合而成的立体图形,其左视图是( )组卷:39引用:2难度:0.8
2.如图是由5个相同的小正方体组合而成的立体图形,其左视图是( )组卷:39引用:2难度:0.8 -
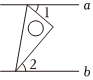 3.已知直线a∥b,将一块含60°角的直角三角板按如图方式放置,其中60°角的顶点在直线a上,30°角的顶点在直线b上,若∠1=40°,则∠2的度数是( )组卷:251引用:4难度:0.8
3.已知直线a∥b,将一块含60°角的直角三角板按如图方式放置,其中60°角的顶点在直线a上,30°角的顶点在直线b上,若∠1=40°,则∠2的度数是( )组卷:251引用:4难度:0.8 -
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
组卷:365引用:5难度:0.9 -
5.不等式组
的解集在数轴上表示正确的是( )3-x≥12x>-2组卷:560引用:11难度:0.7 -
6.下列说法中正确的是( )
组卷:306引用:3难度:0.9 -
7.市政府为了贯彻落实“把绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展荒山绿化,打造美好家园,促进旅游发展.某工程队承接了90万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了任务.设原计划每天绿化的面积为x万平方米,则所列方程正确的是( )
组卷:788引用:12难度:0.8 -
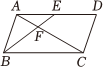 8.如图,点E是▱ABCD的边AD的中点,BE平分∠ABC交AC于点F,下列结论不正确的是( )组卷:79引用:4难度:0.6
8.如图,点E是▱ABCD的边AD的中点,BE平分∠ABC交AC于点F,下列结论不正确的是( )组卷:79引用:4难度:0.6
三、解答题(本大题共9个小题,共72分.解答应写出文字说明、证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.)
-
24.(1)操作发现:在综合实践课上,同学们进行正方形图形变换探究活动,如图1,四边形ABCD和四边形AEFG都是正方形,点E在CD上运动,在AD上截取AH,使AH=DE,连接GH.
①发现:△ADE≌△GHA,请证明;
②推断:线段GH与AB的关系是 .
(2)探究拓展:如图2,四边形ABCD和四边形AEFG都是矩形,点E在CD上运动,,在AD上截取AH,使AH=kDE,连接GH.判断线段GH与AB的关系并证明;AGAE=ABAD=k
(3)学以致用:在(2)的条件下,连接BH交AE于点M,连接FH并延长交AE于点P(如图3).当k=时,若∠FHG=2∠ABH,AB=54,求PM的长.25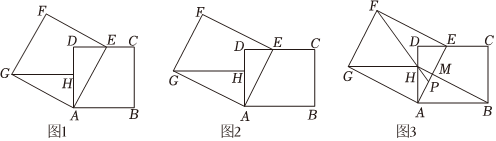 组卷:455引用:1难度:0.2
组卷:455引用:1难度:0.2 -
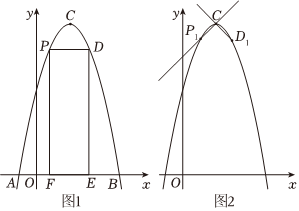 25.如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,顶点为C.
25.如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,顶点为C.
(1)求抛物线的解析式及点C的坐标;
(2)点P是抛物线上位于对称轴左侧x轴上方的一个动点.过点P作x轴的平行线交抛物线于点D,作x轴的垂线交x轴于点F,过点D作x轴的垂线交x轴于点E,四边形PDEF的周长为l:
①当l最大时,求点P的坐标;
②如图2,当l最大时点P,D的位置分别记为P1,D1,将抛物线y=-x2+bx+c平移,使其顶点始终在直线CP1上,当平移后的抛物线与射线D1C只有一个公共点时,设此时抛物线的顶点横坐标为n,求n的取值范围.组卷:236引用:1难度:0.2


