当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省扬州市梅岭教育集团八年级（下）期中数学试卷

发布：2024/7/16 8:0:9

一、选择题（本大题共8小题，每小题3分，共24分，每小题仅有一个答案正确，请把你认为正确的答案填写在答题纸相应位置。）

1．下列图形中，既是轴对称图形，又是中心对称图形的是（　　）
A． B． C． D．
组卷：40引用：1难度：0.9
解析
2．下列代数式中，属于分式的是（　　）
A．
x
-
2
3
B．
x
π
C．
2
x
+
3
D．
1
2
组卷：95引用：2难度：0.8
解析
3．下列是最简二次根式的是（　　）
A．
1
3
B．
9
C．
1
5
D．
2
组卷：153引用：2难度：0.5
解析
4．若分式
x
+
y
3
xy
中的x和y都扩大3倍，那么分式的值（　　）
A．扩大3倍 B．不变 C．缩小9倍 D．缩小3倍
组卷：386引用：3难度：0.5
解析
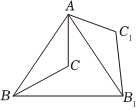5．如图，△ABC绕点A按逆时针方向旋转68°后与△AB₁C₁重合，连接BB₁，则∠ABB₁=（　　）
A．56° B．58° C．62° D．68°
组卷：305引用：5难度：0.5
解析
6．估计
（
12
+
6
）
÷
3
的值应在（　　）
A．2和3之间 B．3和4之间 C．4和5之间 D．5和6之间
组卷：108引用：5难度：0.7
解析
7．化简
（
1
-
a
）
1
a
-
1
的结果是（　　）
A．
1
-
a
B．
-
a
-
1
C．
-
1
-
a
D．
a
-
1
组卷：674引用：4难度：0.6
解析
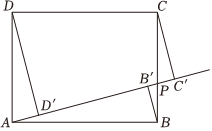8．如图，已知矩形ABCD中，AB=4，AD=3．点P为BC上任意一点（可与点B或C重合），分别过B、C、D作射线AP的垂线，垂足分别是B′、C′、D′，则BB′+CC′+DD′的最小值是（　　）
A．5 B．
12
5
C．
24
5
D．
12
5
5
组卷：408引用：1难度：0.5
解析

二.填空题（本大题共10小题，每小题3分，共30分，请把你认为正确的答案填写在答题纸相应位置。）

9．在函数
y
=
x
-
3
x
-
4
中，自变量x的取值范围是

．
组卷：493引用：38难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共10小题，共96分，解答应写出必要的文字说明、证明过程或演算步骤，请把答案填写在答题纸相应位置。）

27．我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”．数学中，数和形是两个最主要的研究对象，它们之间有着十分密切的联系，在一定条件下，数和形之间可以相互转化，相互渗透．某校数学兴趣小组，在学习完勾股定理和实数后，进行了如下的问题探索与分析．
【提出问题】已知0＜x＜1，求
1
+
x
2
+
1
+
（
1
-
x
）
2
的最小值．
【分析问题】由勾股定理，可以通过构造直角三角形的方法，来分别表示长度为
1
+
x
2
和
1
+
（
1
-
x
）
2
的线段，将代数求和转化为线段求和问题．
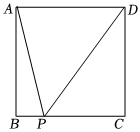
（1）如图，我们可以构造边长为1的正方形ABCD，P为BC边上的动点．设BP=x,则
PC=1-x.则
1
+
x
2
+
1
+
（
1
-
x
）
2
的最小值等于
．
（2）运用以上数形结合的方法，求
9
+
x
2
+
1
+
（
6
-
x
）
2
的最小值；
（3）运用以上数形结合的方法，求
x
2
+
9
-
x
2
-
12
x
+
37
的最大值．
组卷：318引用：1难度：0.5
解析
28．实践操作
在矩形ABCD中，AB=4，AD=3，现将纸片折叠，点D的对应点记为点P，折痕为EF（点E、F是折痕与矩形的边的交点），再将纸片还原．
初步思考
（1）若点P落在矩形ABCD的边AB上（如图①）．
当点P与点A重合时，∠DEF=
°；当点E与点A重合时，∠DEF=
°；
深入探究
（2）当点E在AB上，点F在DC上时（如图②），求证：四边形DEPF为菱形，并直接写出当
AP
=
7
2
时的菱形EPFD的边长．
拓展延伸
（3）若点F与点C重合，点E在AD上，射线BA与射线FP交于点M（如图③）．在折叠过程中，是否存在使得线段AM与线段DE的长度相等的情况？若存在，请求出线段AE的长度；若不存在，请说明理由．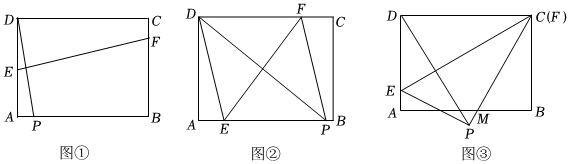
组卷：1986引用：13难度：0.5
解析