2022-2023学年江苏省镇江市扬中第二高级中学高一（下）期末数学试卷

一、单选题：本大题共8小题，每题5分，共40分.在每小题提供的四个选项中，只有一项是符合题目要求的.

• 1．复数z满足z（1+i）=|1-

  3

  i|，则复数z=（　　）

  A． 2 （cos π 4 +isin π 4 ）	B． 2 （cos 3 π 4 +isin 3 π 4 ）
  C． 2 （cos π 4 -isin π 4 ）	D． 2 （cos 7 π 4 -isin 7 π 4 ）
  组卷：55引用：4难度：0.7

  解析

• 2．已知非零向量

  a

  ，

  b

  满足

  b

  =（

  3

  ，1），＜

  a

  ，

  b

  ＞=

  π

  3

  ，若（

  a

  -

  b

  ）⊥

  a

  ，则向量

  a

  在向量

  b

  方向上的投影向量为（　　）

  A． 1 4 b

  B． 1 2 b

  C． 3 2 b

  D． b
  组卷：513引用：7难度：0.7

  解析

• 3．正三棱锥P-ABC的高为2，侧棱与底面所成的角为45°，则点A到侧面PBC的距离是（　　）

  A． 5

  B． 2 2

  C． 2

  D． 6 5 5
  组卷：148引用：6难度：0.7

  解析

• 4．若圆周率π的近似值可以表示成4cos38°，则

  π

  16

  -

  π

  2

  1

  -

  2

  sin

  2

  7

  °

  的近似值为（　　）

  A． 1 8

  B． - 1 8

  C．8

  D．-8
  组卷：173引用：3难度：0.8

  解析

• 5．正四棱台的上、下底面的边长分别为2，4，侧棱长为2，则其体积为（　　）

  A．20+12 3

  B．28 2

  C． 56 3

  D． 28 2 3
  组卷：4899引用：23难度：0.7

  解析

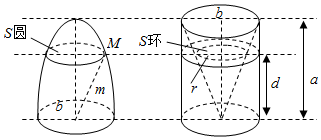• 6．祖暅（公元前5-6世纪），祖冲之之子，是我国齐梁时代的数学家．他提出了一条原理：“幂势既同，则积不容异．”这句话的意思是两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体的体积相等，该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现，比祖暅晚一千一百多年．椭球体是椭圆绕其轴旋转所成的旋转体．如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上．以平行于平面β的平面距平面β任意高d处可横截得到S_圆及S_环两截面，可以证明S_圆=S_环总成立．据此，短轴长为4，长轴长为6的椭球体的体积是（　　）

  A．8π

  B．12π

  C．16π

  D．24π
  组卷：137引用：2难度：0.8

  解析

• 7．三棱锥P-ABC的所有顶点都在球O的球面上．棱锥P-ABC的各棱长为：PA=2，PB=3，PC=4，AB=

  13

  ，BC=5，AC=2

  5

  ，则球O的表面积为（　　）

  A．28π

  B．29π

  C．30π

  D．31π
  组卷：204引用：4难度：0.6

  解析

、解答题：本大题共6小题，共70分，请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.

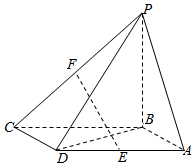• 21．如图，四棱锥P-ABCD的底面ABCD是平行四边形，BA=BD=

  2

  ，AD=2，PA=PD=

  5

  ，E，F分别是棱AD，PC的中点．
  （Ⅰ）证明EF∥平面PAB；
  （Ⅱ）若二面角P-AD-B为60°，
  （i）证明平面PBC⊥平面ABCD；
  （ii）求直线EF与平面PBC所成角的正弦值．
  组卷：3085引用：14难度：0.1

  解析

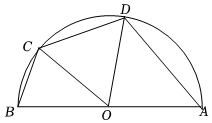• 22．浙江杭州即将举办2022年亚运会，举办方为给运动员创造温馨舒适的居住环境，进行精心设计．如图，是一个以AB为直径的半圆形湖，AB=8（单位：百米），现在设计一个以AB为边的四边形ABCD，C，D在半圆上，设∠BOC=θ（O为圆心）．
  （1）在四边形ABCD内种植荷花，且

  ∠

  COD

  =

  π

  3

  ，当θ为何值时，荷花种植面积最大？
  （2）为了显示美感，景观要错落有致的，要沿BC，CD和DA建造观景栈桥，且BC=CD，当θ为何值时，观景栈桥总长L最长？并求L的最大值．
  组卷：138引用：6难度：0.6

  解析