2022-2023学年北京市东城区景山学校八年级（下）期末数学试卷

一、选择题（本题共16分，每小题2分）

• 1．函数y=

  1

  x

  -

  3

  中，自变量x的取值范围是（　　）

  A．x＞3

  B．x＜3

  C．x=3

  D．x≠3
  组卷：957引用：11难度：0.9

  解析

• 2．点A（1，y₁），B（3，y₂）是反比例函数y=

  -

  6

  x

  图象上的两点，那么y₁，y₂的大小关系是（　　）

  A．y1＞y2

  B．y1=y2

  C．y1＜y2

  D．不能确定
  组卷：547引用：21难度：0.9

  解析

• 3．如图，在Rt△ABC中，∠ACB=90°，如果AC=3，AB=5，那么sinB等于（　　）

  A． 3 5

  B． 4 5

  C． 3 4

  D． 4 3
  组卷：419引用：8难度：0.9

  解析

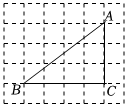• 4．如图，每个小正方形的边长为1，点A、B、C均在格点上，则sinB的值是（　　）

  A．1

  B． 3 4

  C． 4 5

  D． 3 5
  组卷：188引用：1难度：0.5

  解析

• 5．如图，已知正方形ABCD，以点A为圆心，AB长为半径作⊙A，点C与⊙A的位置关系为（　　）

  A．点C在⊙A外

  B．点C在⊙A内

  C．点C在⊙A上

  D．无法确定
  组卷：302引用：7难度：0.7

  解析

• 6．如图，四边形ABCD内接于⊙O，若∠C=130°，则∠BOD的度数为（　　）

  A．50°

  B．100°

  C．130°

  D．150°
  组卷：2698引用：38难度：0.6

  解析

• 7．如图，在⊙O中，弦AB垂直平分半径OC．若⊙O的半径为4，则弦AB的长为（　　）

  A． 2 3

  B． 4 3

  C． 2 5

  D． 4 5
  组卷：530引用：3难度：0.9

  解析

• 8．下面两个问题中都有两个变量：
  ①矩形的周长为20，矩形的面积y与一边长x；
  ②矩形的面积为20，矩形的宽y与矩形的长x.
  其中变量y与变量x之间的函数关系表述正确的是（　　）

  A．①是反比例函数，②是二次函数

  B．①是二次函数，②是反比例函数

  C．①②都是二次函数

  D．①②都是反比例函数
  组卷：389引用：3难度：0.7

  解析

二、填空题（本题共16分，每小题2分）

• 9．已知反比例函数y=

  m

  -

  1

  x

  的图象分布在第二、四象限，则m的取值范围是

  ．
  组卷：554引用：8难度：0.6

  解析

三、解答题（本题共68分）

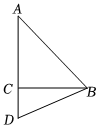• 27．如图，△ABC是等腰直角三角形，∠ACB=90°，AC=BC，D为AC延长线上一点，连接BD，将线段BD绕点D逆时针旋转90°得到线段DE，过点E作EF⊥AC于点F，连接AE．
  （1）依题意补全图形；
  （2）比较AF与CD的大小，并证明；
  （3）连接BE，G为BE的中点，连接CG，用等式表示线段CD，CG，BC之间的数量关系，并证明．
  组卷：1324引用：5难度：0.2

  解析

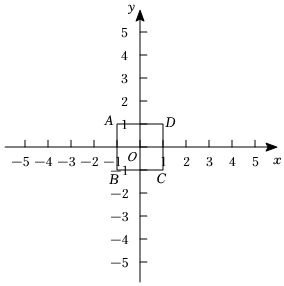• 28．已知点M和图形W，Q为图形W上一点，若存在点P，使得点M为线段PQ的中点（P，Q不重合），则称点P为图形W关于点M的倍点．
  如图，在平面直角坐标系xOy中，点A（-1，1），B（-1，-1），C（1，-1），D（1，1）．
  （1）若点M的坐标为（2，0），则在P₁（3，0），P₂（4，2），P₃（5，1）中，是正方形ABCD关于点M的倍点的是

  ；
  （2）点N的坐标为（2，t），若在直线y=x上存在正方形ABCD关于点N的倍点，直接写出t的取值范围；
  （3）点G为正方形ABCD边上一动点，直线y=x+b与x轴交于点E，与y轴交于点F，若线段EF上的所有点均可成为正方形ABCD关于点G的倍点，直接写出b的取值范围．
  组卷：1319引用：6难度：0.3

  解析