2022-2023学年北京市东城区汇文中学八年级（下）期中数学试卷

一、选择题（每小题2分，共20分）

• 1．下列各式中，哪个是最简二次根式（　　）

  A． 0 . 2

  B． 1 2

  C． 5

  D． 12
  组卷：225引用：11难度：0.8

  解析

• 2．以下列各数为边长，能构成直角三角形的是（　　）

  A．1，2，2

  B．1， 3 ，2

  C．4，5，6

  D．1，1， 3
  组卷：357引用：12难度：0.6

  解析

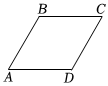• 3．如图，平行四边形ABCD中，若∠B=2∠A，则∠C的度数为（　　）

  A．60°

  B．120°

  C．72°

  D．36°
  组卷：468引用：10难度：0.7

  解析

• 4．下列计算中，正确的是（　　）

  A． 2 × 3 = 6

  B． 2 + 2 = 2 2

  C． 2 3 - 2 = 3

  D． 2 + 3 = 5
  组卷：134引用：6难度：0.6

  解析

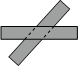• 5．如图，两把完全一样的直尺叠放在一起，重合的部分构成一个四边形，这个四边形一定是（　　）

  A．矩形

  B．菱形

  C．正方形

  D．无法判断
  组卷：367引用：44难度：0.6

  解析

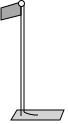• 6．如图在实践活动课上，小华打算测量学校旗杆的高度，她发现旗杆顶端的绳子垂到地面后还多出1m,当她把绳子斜拉直，且使绳子的底端刚好接触地面时，测得绳子底端距离旗杆底部5m,由此可计算出学校旗杆的高度是（　　）

  A．8m

  B．10m

  C．12m

  D．15m
  组卷：1451引用：13难度：0.6

  解析

• 7．如图，一支铅笔放在圆柱体笔筒中，笔筒的内部底面直径是9cm,内壁高12cm,则这支铅笔的长度可能是（　　）

  A．9cm

  B．12cm

  C．15cm

  D．18cm
  组卷：1741引用：20难度：0.7

  解析

• 8．下列命题正确的是（　　）

  A．一组对边平行，另一组对边相等的四边形是平行四边形

  B．对角线相等的四边形是矩形

  C．有一组邻边相等的四边形是菱形

  D．有一组邻边相等且有一个角是直角的平行四边形是正方形
  组卷：658引用：21难度：0.7

  解析

• 9．如图，在△ABC中，点D、点E分别是AB，AC的中点，点F是DE上一点，且∠AFC=90°，若BC=12，AC=8，则DF的长为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：2414引用：20难度：0.6

  解析

三、解答题（共64分）

• 27．现有正方形ABCD和一个直角∠MON．
  
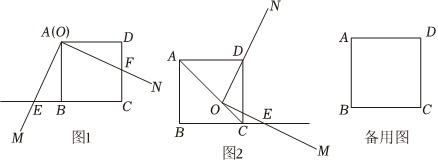
  （1）如图1，若点O与点A重合，射线OM交CB延长线于E，射线ON交正方形的边CD于F，则OE与OF的数量关系是

  ，请证明你的结论；
  （2）如图2，若点O在正方形的对角线AC上，射线OM交BC延长线于E，射线ON恰好经过点D，则CB、CE与CO的数量关系是

  ，请证明你的结论；
  （3）若∠MON在正方形ABCD所在平面内任意移动，射线OM交直线BC于点E，射线ON交直线CD于点F，若OE与OF始终保持相等，请你直接写出点O所有可能的位置．
  组卷：214引用：2难度：0.5

  解析

• 28．在平面直角坐标系xOy中，对于P，Q两点，给出如下定义：若点P到x、y轴的距离中的最大值等于点Q到x、y轴的距离中的最大值，则称P，Q两点为“等距点”．
  
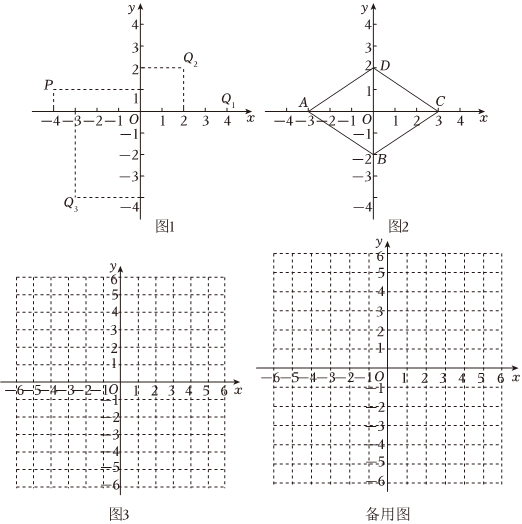
  （1）如图1，已知点P的坐标为（-4，1），在点Q₁（4，0），Q₂（2，2），Q₃（-3，-4）中，与点P是“等距点”的有

  ；
  （2）如图2，菱形ABCD四个顶点的坐标为A（-a,0），B（0，-b），C（a,0），D（0，b），（a＞0，b＞0），
  ①当a=b=5时，点N为菱形的边CD上一个动点，令点N到x、y轴的距离中的最大值为d_N，则d_N的取值范围是

  ；
  ②当a=6，b=3时，点F为菱形的边CD上一个动点，若平面中存在一点E，使得E，F两点为“等距点”．在图3中画出点E的轨迹，并计算该轨迹所形成图形的面积；
  ③我们规定：横纵坐标均为整数的点是整点．若菱形ABCD的边CD过定点（1，1），点F为菱形的边CD上一个动点，平面中存在一点E，使得E，F两点为“等距点”，若菱形内部（不含边界）恰有9个整点，直接写出点E的轨迹所覆盖整点的个数．
  组卷：156引用：2难度：0.2

  解析