2022-2023学年上海市浦东新区建平中学高一（下）期末数学试卷

一、填空题：（1-6题每题4分，7-12题每题5分，共54分）

• 1．在△ABC中，AB=3，BC=5，AC=7，则角B的余弦值是

  ．
  组卷：69引用：1难度：0.8

  解析

• 2．已知点P（3，1），Q（2，4），则直线PQ的一般式方程为

  ．
  组卷：184引用：1难度：0.8

  解析

• 3．函数y=3sinx-acosx（a＞0）的最大值为

  10

  ，则正数a的值是

  ．
  组卷：39引用：1难度：0.7

  解析

• 4．已知i是虚数单位，若复数z=i•（1+i），则|z|=

  ．
  组卷：221引用：3难度：0.8

  解析

• 5．若

  a

  =

  （

  1

  ，

  2

  ）

  ，

  b

  =

  （

  3

  ，-

  4

  ）

  ，则

  a

  在

  b

  方向上的数量投影为

  ．
  组卷：41引用：1难度：0.7

  解析

• 6．已知i为虚数单位，复数

  2

  1

  -

  i

  的共轭复数为

  ．
  组卷：27引用：3难度：0.8

  解析

• 7．已知数列{a_n}的前n项和S_n=n²+1，那么它的通项公式为a_n=

  ．
  组卷：530引用：6难度：0.7

  解析

三、解答题：（17，18，19题每题14分，20，21题每题18分，共78分）

• 20．已知点P和非零实数λ，若两条不同的直线l₁，l₂均过点P，且斜率之积为λ，则称直线l₁，l₂是一组“P_λ共轭线对”，如直线l₁：y=2x和l₂：y=

  -

  1

  2

  x

  是一组“O_-1共轭线对”，其中O是坐标原点．
  （1）已知l₁、l₂是一组“O_-3共轭线对”，求l₁，l₂的夹角的最小值；
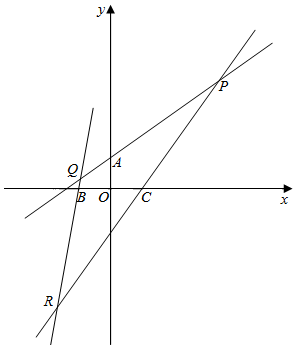
  （2）已知点A（0，1）、点B（-1，0）和点C（1，0）分别是三条直线PQ，QR，RP上的点（A，B，C与P，Q，R均不重合），且直线PR，PQ是“P₁共轭线对”，直线QP，QR是“Q₄共轭线对”，直线RP，RQ是“R₉共轭线对”，求点P的坐标；
  （3）已知点Q（-1，-

  2

  ），直线l₁，l₂是“Q_-2共轭线对”，当l₁的斜率变化时，求原点O到直线l₁、l₂的距离之积的取值范围．
  组卷：230引用：9难度：0.5

  解析

• 21．在平面直角坐标系xOy中，已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的最小正周期为π，且直线x=-

  π

  2

  是其图象的一条对称轴．
  （1）求函数f（x）的解析式；
  （2）将函数y=f（x）的图象向右平移

  π

  4

  个单位，再将所得的图象上每一点的纵坐标不变，横坐标伸长为原来的2倍后所得到的图象对应的函数记作y=g（x）．
  ①若动点

  Q

  （

  f

  （

  α

  2

  ）

  ，

  g

  （

  α

  ）

  ）

  在圆O上运动，P为圆O外一点，过点P作圆O的两条切线，切点分别为M，N，求

  PM

  •

  PN

  的最小值；
  ②已知常数λ∈R，n∈N^*，

  α

  =

  （

  cosx

  -

  sinx

  ,

  λ

  ）

  ，

  β

  =

  （

  cosx

  +

  sinx

  ,

  g

  （

  x

  ）

  ）

  ，且函数

  F

  （

  x

  ）

  =

  α

  •

  β

  在（0，π）内恰有2023个零点，求常数λ与n的值．
  组卷：195引用：2难度：0.3

  解析