2023年江苏省泰州市靖江市中考数学二模试卷

一、选择题（本大题共有6小题，每小题3分，共18分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）

• 1．下列四个数中，是负数的是（　　）

  A．|-3|

  B．-（-3）

  C．（-3）2

  D．-3
  组卷：351引用：3难度：0.8

  解析

• 2．下列图形中既是中心对称图形又是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：77引用：5难度：0.9

  解析

• 3．下列运算结果错误的是（　　）

  A．m3÷m2=m

  B．（m2）3=m6

  C．m2•m3=m5

  D．m2+m3=m5
  组卷：39引用：1难度：0.8

  解析

• 4．在平面直角坐标系中，把一个多边形的所有顶点坐标（其中有一个顶点为原点、有一条边在横坐标轴上）分别乘以-

  1

  2

  所对应的图形与原图形是（　　）

  A．位似变换

  B．旋转变换

  C．轴对称变换

  D．平移变换
  组卷：57引用：1难度：0.8

  解析

• 5．对于数据：2、2、5、3、7、5、5．下列统计量不能在原数据中找出的是（　　）

  A．极差

  B．平均数

  C．中位数

  D．众数
  组卷：46引用：3难度：0.6

  解析

• 6．已知抛物线y=-x²-4mx+m²-1，A（-2m-4，y₁），B（m+3，y₂）为该抛物线上的两点，若y₁＜y₂，则m的取值范围（　　）

  A．m＜ - 7 3	B．m＞ 1 3
  C．m＜ - 7 3 或m＞ 1 3	D． - 7 3 ＜m＜ 1 3
  组卷：223引用：1难度：0.5

  解析

二、填空题（本大题共有10小题，每小题3分，共30分．请把答案直接填写在答题卡相应位置上）

• 7．2023年5月6日，“五一”消费数据出炉，国内旅游收入约148000000000元，将数据148000000000用科学记数法表示为

  ．
  组卷：56引用：2难度：0.9

  解析

• 8．二次根式

  x

  -

  4

  中x的取值范围是

  ．
  组卷：62引用：4难度：0.8

  解析

三、解答题（本大题共有10题，共102分.请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）

• 25．【问题情境】
  综合与实践课上，老师让同学们以“正方形纸片折叠的方式，探索tan22.5°及tan15°”为主题开展数学活动，下面是同学们的折纸过程．【操作过程】
  （1）如图1，先将正方形纸片沿对角线折叠，折痕为BD．将点C翻折到BD上的点F处，且使折痕过点B，则∠EBC=∠EBF=22.5°，则tan22.5°=

  ；
  （2）为构造15°，同学们积极动脑并进行如下操作：如图2，将正方形纸片翻折，使得点A与点D、点B与点C重合，折痕为GH．展开后，将点C翻折到GH上的点R处，且使折痕过点B，连接BR．再将点A翻折到GH上的点R处，折痕为BK．根据以上操作请你求出tan15°的值；
  【探索发现】
  （3）如图3，在图2的基础上，同学们通过其他折叠方式在CD上找到一点P，使得∠PBC=15°，连接KP，发现S_△ABK与S_△DKP存在固定不变的数量关系，请写出你的猜想并验证．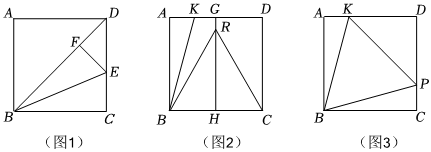
  组卷：127引用：2难度：0.1

  解析

• 26．定义（a,b,c）为函数y=ax²+bx+c的“特征数”．如：函数y=2x²-3x+5的“特征数”是（2，-3，5），函数y=x+2的“特征数”是（0，1，2），函数y=-2x的“特征数”是（0，-2，0）．
  （1）若一个函数y₁的特征数是（0，k,6）（k为常数，且k≠0），将此函数的图象向下平移6个单位得到一个图象对应的函数y₂“特征数”是

  ；
  （2）若将一个函数关于y轴对称得到的对应函数y₃的特征数是（1，-4，3），则原函数的特征数是

  ．
  A．（-1，-4，-3）
  B．（-1，4，-3）
  C．（1，4，3）
  D．（1，4，-3）
  （3）若（2）中对应函数y₃上有两点A（m+2，n₁），B（2m+1，n₂），其中A在B的左侧，当m为整数时，

  n

  2

  n

  1

  也为整数，求m的值；
  （4）若（1）中的函数y₂与（2）中的函数y₃交于C，D两点，在y轴正半轴上是否存在一点P（0，p），分别与C，D两点连接，构造特征数是（0，a,p），（0，b,p）的函数，当k取不为0的任意实数时，都能使得a+b为定值．若存在，求出P点坐标及这个定值，若不存在请说明理由．
  组卷：202引用：2难度：0.2

  解析