2022-2023学年湖北省武汉市江夏区建新中学九年级（上）第三次月考数学试卷

一、选择题（共30分）

• 1．将一元二次方程x²-4=5x化为一般形式后，其中二次项系数、一次项系数分别是（　　）

  A．1，5

  B．1，-5

  C．-4，5

  D．-4，-5
  组卷：81引用：5难度：0.9

  解析

• 2．以下是新冠病毒防范宣传图标，其中为中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：14引用：3难度：0.8

  解析

• 3．已知⊙O的半径等于5，点P在直线l上，圆心O到点P的距离为5，那么直线l与⊙O的位置关系是（　　）

  A．相切

  B．相交

  C．相切或相离

  D．相交或相切
  组卷：101引用：3难度：0.5

  解析

• 4．抛物线y=-x²经过平移后得到y=-（x+2）²-3，其平移方法是（　　）

  A．向右平移2个单位，再向下平移3个单位

  B．向右平移2个单位，再向上平移3个单位

  C．向左平移2个单位，再向下平移3个单位

  D．向左平移2个单位，再向上平移3个单位
  组卷：681引用：7难度：0.6

  解析

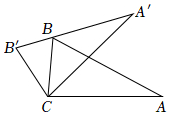• 5．如图，将△ABC绕顶点C逆时针旋转角度α得到△A'B'C'，且点B刚好落在A'B'上．若∠A=26°，∠BCA'=44°，则α等于（　　）

  A．37°

  B．38°

  C．39°

  D．40°
  组卷：704引用：14难度：0.7

  解析

• 6．如图，矩形相框长为8cm宽为4cm,四周的边框宽相等，且照片的面积占总面积的

  3

  4

  ，设四周边框的宽是x cm,根据题意可列方程为（　　）

  A． （ 8 x + 4 x ） × 2 = 1 4 × 8 × 4	B． （ 8 - 2 x ） （ 4 - 2 x ） = 3 4 × 8 × 4
  C． （ 8 - 2 x ） （ 4 - 2 x ） = 1 4 × 8 × 4	D． 8 × 4 - 8 x - 4 x - 4 x 2 = 3 4 × 8 × 4
  组卷：55引用：3难度：0.6

  解析

• 7．如图，AB是⊙O的直径，C、D、E是⊙O上的点，若

  ˆ

  AD

  =

  ˆ

  DC

  ，∠E=70°，则∠ABC的度数（　　）

  A．30°

  B．40°

  C．50°

  D．60°
  组卷：531引用：7难度：0.7

  解析

• 8．关于x的一元二次方程（k-1）x²-2x+1=0总有实数根，则k应满足的条件是（　　）

  A．k≤2

  B．k≤2且k≠1

  C．k＜2且k≠1

  D．k≥2
  组卷：309引用：11难度：0.7

  解析

三、解答题（共72分）

• 23．已知∠ABN=90°，在∠ABN内部作等腰△ABC，AB=AC，∠BAC=α（0°＜α＜90°）．点D为射线BN上任意一点，连接AD，将线段AD绕点A逆时针旋转α得到线段AE，连接EC并延长交射线BN于点F．
  
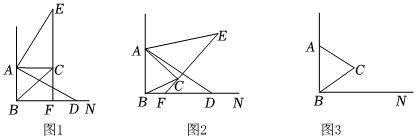
  （1）如图1，当α=90°时，试探究线段BF与CF的数量关系并证明；
  （2）如图2，当0°＜α＜90°时，（1）中的结论是否还成立？若成立，请给予证明；若不成立，请说明理由；
  （3）若α=60°，

  AB

  =

  4

  3

  ，当点D在直线BN上运动的过程中，请直接写出BE的最小值是

  ．
  组卷：170引用：3难度：0.1

  解析

• 24．如图，抛物线y=

  1

  2

  x²-2x-6与x轴相交于点A、点B，与y轴相交于点C．
  （1）请直接写出点A，B，C的坐标；
  （2）点P（m,n）（0＜m＜6）在抛物线上，当m取何值时，△PBC的面积最大？并求出△PBC面积的最大值．
  （3）点F是抛物线上的动点，作FE∥AC交x轴于点E，是否存在点F，使得以A、C、E、F为顶点的四边形是平行四边形？若存在，请写出所有符合条件的点F的坐标；若不存在，请说明理由．
  
  组卷：2007引用：20难度：0.1

  解析