2022-2023学年广东省深圳市宝安区松岗中学八年级（下）期中数学试卷
发布：2024/5/23 8:0:8
一、选择题（本题共有10小题，每小题3分，共30分，每小题有四个选项，其中只有一个正确的）
-
1．三角形的三边长分别为a、b、c,则下面四种情况中，不能判断此三角形为直角三角形的是（ ）
组卷：330引用：6难度：0.7 -
2．不等式3+2x＜1的解集在数轴上表示正确的是 （ ）
组卷：508引用：10难度：0.8 -
3．下列各式中，从左到右的变形是因式分解的是（ ）
组卷：376引用：5难度：0.7 -
4．在下列不等式组中，无解的是（ ）
组卷：1075引用：9难度：0.8 -
5．在下列正多边形中，既是轴对称图形，又是中心对称图形的是（ ）
组卷：145引用：6难度：0.8 -
6．下面是小明解不等式
的过程：x+52-1＜3x+22
解：去分母，得x+5-1＜3x+2…①
移项，得x-3x＜2-5+1…②
合并同类项，得-2x＜-2…③
两边同时除以-2，得x＜1…④
小明的计算过程中，没掌握好基本知识或粗心出错的步骤是（ ）组卷：1050引用：11难度：0.7 -
7．如图，在△ABC和△BAD中，∠C=∠D=90°．在以下条件：①AC=BD；②AD=BC；③∠BAC=∠ABD；④∠ABC=∠BAD；⑤∠CAD=∠DBC中，再选一个条件，就能使△ABC≌△BAD，共有（ ）选择．组卷：1360引用：7难度：0.4 -
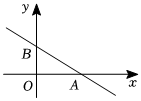8．如图，一次函数y=kx+b（k≠0）的图象分别与x轴、y轴相交A（3，0）、点B（0，2），则下列说法不正确的是（ ）组卷：796引用：7难度：0.6
五、解答题三（本题共2小题，共19分）
-
24．如图（1），已知CA=CB，CD=CE，且∠ACB=∠DCE，将△DCE绕C点旋转（A、C、D三点在同一直线上除外）．
（1）求证：△ACD≌△BCE；
（2）在△DCE绕C点旋转的过程中，若ED、AB所在的直线交于点F，当点F为边AB的中点时，如图2所示．求证：∠ADF=∠BEF（提示：利用类倍长中线方法添加辅助线）；
（3）在（2）的条件下，求证：AD⊥CD．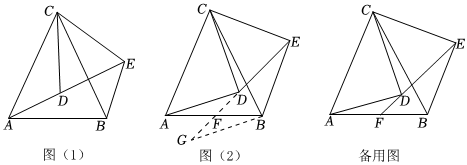
组卷：1135引用：12难度：0.3 -
25．【问题背景】
在图（1）中，①～③的三个三角形，各自是由△ABC通过怎样的全等变换得到的？
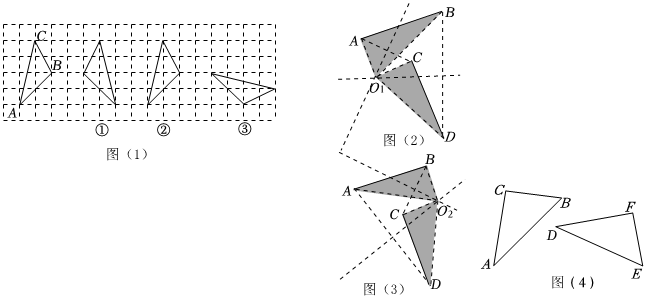【问题探究】
（1）我们发现：
Ⅰ：图（1）中，①号三角形能由△ABC通过一次轴对称得到，请在图（1）中画出对称轴．
Ⅱ：图（1）中，②号三角形能由△ABC通过一次平移得到，则平移的距离为 单位．
Ⅲ：图（1）中，③号三角形能由△ABC通过先平移再旋转或先旋转再平移得到，请问：③号三角形能否由△ABC绕某个点，旋转一次得到？为解决这个问题，我们可以先解决两条相等的线段能否看成：一条线段是另一条线段绕某个点旋转一次得到．分析过程如下：
已知线段AB与线段CD相等，分两种情况讨论：
第一种情况：当AB与CD对应时，如图（2），分别作AC与BD的中垂线交于点O1，连接O1A、O1C、O1B、O1D．
∵O1在AC的中垂线上
∴O1A=O1C
同理，O1B=O1D
又∵AB=CD
∴△ABO1≌△CDO1（SSS）
∴∠AO1B=∠CO1D
∴∠AO1C=∠BO1D，即对应点与点O1形成的夹角相等
∴线段CD可以看成由线段AB绕点O1旋转一次得到.
第二种情况：当AB与DC对应时，如图（3），同理可证．
综上所述：两条相等的线段可以看成：一条线段是另一条线段绕某个点旋转一次得到．
【问题解决】
（2）如图（4），已知△ABC≌△DEF（且满足△DEF不能由△ABC通过平移得到）．现在来解决△DEF能由△ABC绕某个点通过一次旋转得到的问题：
①通过尺规作图找到旋转中心O；
②证明：△DEF能由△ABC绕点O通过一次旋转得到．（提示：只要证明关键的对应点到点O的距离相等和关键的对应点与点O形成的夹角相等）组卷：366引用：5难度：0.2
