2022-2023学年广西大学附中九年级（上）第三次月考数学试卷

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑）

• 1．

  -

  2

  3

  的绝对值是（　　）

  A． 2 3

  B． - 2 3

  C． 3 2

  D． - 3 2
  组卷：329引用：116难度：0.9

  解析

• 2．在如图所示的平面直角坐标系中，小手盖住的点的坐标可能是（　　）
  

  A．（1，2）

  B．（-1，2）

  C．（-1，-2）

  D．（1，-2）
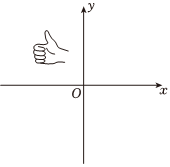  组卷：492引用：6难度：0.5

  解析

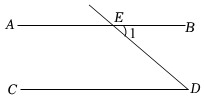• 3．如图，直线AB，CD被直线DE所截，AB∥CD，∠1=40°，则∠D的度数为（　　）

  A．20°

  B．40°

  C．50°

  D．140°
  组卷：331引用：5难度：0.8

  解析

• 4．2022年10月12号，“神舟十四号”飞行乘组，在距地面约390000米的中国空间站问天实验舱开展第三次天宫授课，大大激发了广大青少年的追求科学的兴趣，数据“390000”用科学记数法表示为（　　）

  A．3.9×104

  B．3.9×105

  C．39×104

  D．0.39×106
  组卷：673引用：14难度：0.8

  解析

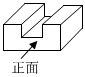• 5．如图所示是一个钢块零件，它的左视图是（　　）

  A．

  B．

  C．

  D．
  组卷：819引用：24难度：0.7

  解析

• 6．下列计算正确的是（　　）

  A．（3a）2=6a2

  B．（a3）2=a6

  C．a6÷a2=a3

  D．a2•a3=a6
  组卷：5引用：3难度：0.7

  解析

• 7．某校有4000名学生，随机抽取了400名学生进行体重调查，下列说法错误的是（　　）

  A．总体是该校4000名学生的体重

  B．个体是每一个学生

  C．样本是抽取的400名学生的体重

  D．样本容量是400
  组卷：2073引用：34难度：0.9

  解析

• 8．周一，小南爸爸开车送小南去上学，匀速行驶了一段后，遇上了早高峰，停滞不前，之后为了不迟到，立即以较快的速度匀速到达学校．在小南爸爸开车送小南过程中x表示小南爸爸开车的时间，y表示他们离学校的距离，下面能反映y与x的关系的大致图象是（　　）

  A．

  B．

  C．

  D．
  组卷：290引用：5难度：0.9

  解析

三、解答题（本大题共8小题，共72分．解答应写出文字说明、证明过程或演算步骤．）

• 25．如图1，抛物线y=ax²+2x+c,交x轴于A、B两点，交y轴于点C，其中点A坐标为（-1，0），点B坐标为（3，0），F为抛物线顶点，直线EF垂直于x轴于点E．
  
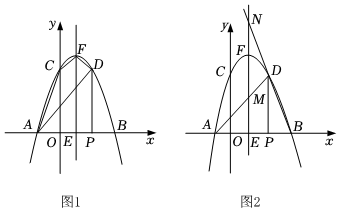
  （1）求抛物线的表达式；
  （2）点P是线段BE上的动点（除B、E外），过点P作x轴的垂线交抛物线于点D．
  ①当点P的横坐标为2时，求四边形ACFD的面积；
  ②如图2，直线AD，BD分别与抛物线对称轴交于M、N两点．试问，EM+EN是否为定值？如果是，请求出这个定值；如果不是，请说明理由．
  组卷：66引用：3难度：0.5

  解析

• 26．矩形ABCD中，

  AB

  BC

  =

  k

  2

  （k＞1），点E是边BC的中点，连接AE，过点E作AE的垂线EF，与矩形的外角平分线CF交于点F．
  【特例证明】
  （1）如图（1），当k=2时，求证：AE=EF；
  小明不完整的证明过程如下，请你帮他补充完整．
  

  证明：如图，在BA上截取BH=BE，连接EH． ∵k=2， ∴AB=BC． ∵∠B=90°，BH=BE， ∴∠1=∠2=45°， ∴∠AHE=180°-∠1=135°． ∵CF平分∠DCG，∠DCG=90°， ∴∠3= 1 2 ∠DCG=45°． ∴∠ECF=∠3+∠4=135°． ∴…… （只需在答题卡对应区域写出剩余证明过程）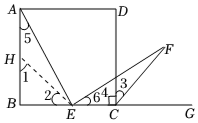

  【类比探究】
  （2）如图（2），当k≠2时，求

  AE

  EF

  的值（用含k的式子表示）；
  【拓展运用】
  （3）如图（3），当k=3时，P为边CD上一点，连接AP，PF，∠PAE=45°，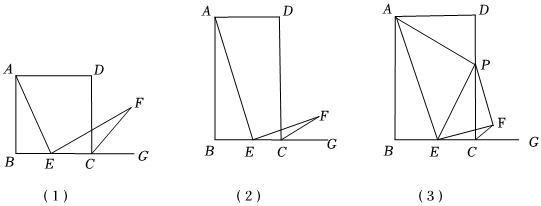

  PF

  =

  5

  ，求BC的长．
  
  组卷：2371引用：6难度：0.2

  解析