2023-2024学年江西省南昌市南昌县八年级（上）期中数学试卷

一、选择题（本大题共8小题，每小题3分，共24分）

• 1．下列图案中，是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：2引用：2难度：0.9

  解析

• 2．已知三角形的三边长分别为4，5，x,则x不可能是（　　）

  A．3

  B．5

  C．7

  D．9
  组卷：842引用：89难度：0.9

  解析

• 3．如图，在△ABC中，∠C=90°，∠B=30°，AD是△ABC的角平分线，DE⊥AB，垂足为E，DE=1，则BC=（　　）

  A． - 3

  B．2

  C．3

  D． - 3 + 2
  组卷：44引用：3难度：0.7

  解析

• 4．在平面直角坐标系中，点A（2，3）与点B关于y轴对称，则点B的坐标为（　　）

  A．（-2，3）

  B．（-2，-3）

  C．（2，-3）

  D．（-3，-2）
  组卷：1491引用：15难度：0.9

  解析

• 5．等腰三角形一内角为100°，则底角度数是（　　）

  A．100°或40°

  B．100°

  C．50°

  D．40°
  组卷：50引用：1难度：0.7

  解析

• 6．已知△ABC的周长是24，且AB=AC，又AD⊥BC，D为垂足，若△ABD的周长是20，则AD的长为（　　）

  A．6

  B．8

  C．10

  D．12
  组卷：614引用：42难度：0.9

  解析

• 7．设M表示直角三角形，N表示等腰三角形，P表示等边三角形，Q表示等腰直角三角形．下列四个图中，能正确表示它们之间关系的是（　　）

  A．

  B．

  C．

  D．
  组卷：1610引用：4难度：0.9

  解析

四、（本大题共3小题，每小题8分，共24分）

• 21．如图所示，根据图中的对话回答问题．
  
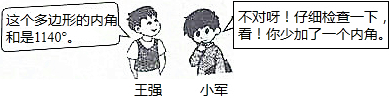
  （1）王强是在求几边形的内角和？
  （2）少加的那个内角为多少度？
  组卷：211引用：6难度：0.6

  解析

五、（本大题共1小题，每小题10分，共10分）

• 22．定义：如图（1），若分别以△ABC的三边AC，BC，AB为边向三角形外侧作正方形ACDE，BCFG和ABMN，则称这三个正方形为△ABC的外展三叶正方形，其中任意两个正方形为△ABC的外展双叶正方形．
  （1）作△ABC的外展双叶正方形ACDE和BCFG，记△ABC，△DCF的面积分别为S₁和S₂．
  ①如图（2），当∠ACB=90°时，求证：S₁=S₂．
  ②如图（3），当∠ACB≠90°时，S₁与S₂是否仍然相等，请说明理由．
  （2）已知△ABC中，AC=3，BC=4，作其外展三叶正方形，记△DCF，△AEN，△BGM的面积和为S，请利用图（1）探究：当∠ACB的度数发生变化时，S的值是否发生变化？若不变，求出S的值；若变化，求出S的最大值．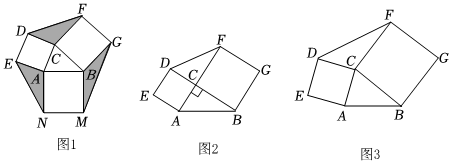
  
  组卷：283引用：9难度：0.5

  解析