2023-2024学年吉林省长春八十七中13-18班八年级（上）月考数学试卷（9月份）

一、选择题（每小题3分，共24分）

• 1．在实数

  22

  7

  ，0.3333…，3.14，

  3

  中，无理数是（　　）

  A． 22 7

  B．0.3333…

  C．3.14

  D． 3
  组卷：60引用：1难度：0.9

  解析

• 2．下列各式是最简二次根式的是（　　）

  A． 1 5

  B． 7 3 2

  C． 1 2

  D．2 8
  组卷：127引用：2难度：0.7

  解析

• 3．下列计算正确的是（　　）

  A． 25 =± 5

  B． - 3 64 = 4

  C． ± 4 = 2

  D． （ 3 - 8 ） 2 = 4
  组卷：130引用：2难度：0.8

  解析

• 4．如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△ABC全等的图形是（　　）
  

  A．甲乙

  B．甲丙

  C．乙丙

  D．乙
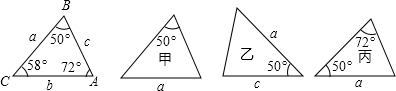  组卷：1053引用：83难度：0.9

  解析

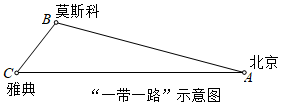• 5．如图，若记北京为A地，莫斯科为B地，雅典为C地，若想建立一个货物中转仓，使其到A、B、C三地的距离相等，则中转仓的位置应选在（　　）

  A．三边垂直平分线的交点	B．三边中线的交点
  C．三条角平分线的交点	D．三边上高的交点
  组卷：2448引用：20难度：0.7

  解析

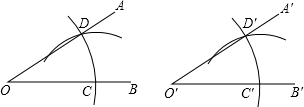• 6．用直尺和圆规作一个角等于已知角，如图，能得出∠A′O′B′=∠AOB的依据是（　　）

  A．（SAS）

  B．（SSS）

  C．（ASA）

  D．（AAS）
  组卷：3762引用：152难度：0.8

  解析

• 7．已知：n＜

  32

  ＜m,且m,n是两个连续整数，则mn=（　　）

  A．28

  B．29

  C．30

  D．31
  组卷：334引用：6难度：0.8

  解析

• 8．如图，在△ABC中，∠A=30°，∠C=90°．下列尺规作图痕迹中，不能将△ABC的面积平分的是（　　）

  A．

  B．

  C．

  D．
  组卷：440引用：8难度：0.5

  解析

三、解答题（共78分）

• 23．教材呈现：下图是华师版八年级上册数学教材第96页的部分内容．
  
  【定理证明】请根据教材中的分析，结合图①，写出“角平分线性质定理”完整的证明过程．
  【定理应用】（1）如图②，在△ABC中，AD、BE分别是∠BAC、∠ABC的角平分线，AD、BE的交点为O．连结CO交AB于点F，则∠ACF与∠BCF的大小关系为

  ．
  （A）∠ACF＞∠BCF．（B）∠ACF＜∠BCF．（C）∠ACF=∠BCF．（D）无法确定．
  （2）如图③，在四边形ABCD中，∠DAB的角平分线与∠ABC的角平分线交于点E，且点E在CD的垂直平分线l上，连结CE、DE，求证：∠ADC=∠BCD．
  
  组卷：110引用：1难度：0.2

  解析

• 24．在△ABC中，AB=18，BC=15，点D为边CB的中点，动点P以每秒2个单位的速度从点B出发在射线BA上运动，点Q在边AC上，设点P运动时间为t秒，（t＞0）
  （1）用含t的代数式表示线段AP的长．
  （2）当AC=BC，点P在线段BA上．
  ①若△BPD和△AQP全等，求t的值；
  ②连结CP，已知△ABC中BC边上的高为14.4，设△ACP的面积为S，当S=12时，求t的值．
  （3）当∠CAB=70°，△AQP为等腰三角形时，请直接写出∠APQ的度数．
  组卷：108引用：1难度：0.2

  解析