2023-2024学年山东省青岛市九年级（上）质检数学试卷（9月份）

一、选择题：（本大题共10个小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．下列四个几何体中，从正面看是三角形的是（　　）

  A．

  B．

  C．

  D．
  组卷：679引用：15难度：0.8

  解析

• 2．下列图形中，既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：172引用：4难度：0.9

  解析

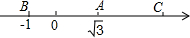• 3．如图的数轴上，点B与点C关于点A对称，A、B两点对应的实数是

  3

  和-1，则点C所对应的实数是（　　）

  A．1 + 3

  B．2 + 3

  C．2 3 -1

  D．2 3 +1
  组卷：1461引用：21难度：0.9

  解析

• 4．下列运算正确的是（　　）

  A．5a2-4a2=1

  B．a7÷a4=a3

  C．（a3）2=a5

  D．a2•a3=a6
  组卷：497引用：5难度：0.8

  解析

• 5．华为麒麟990芯片采用了最新的0.000000007米的工艺制程，数0.000000007用科学记数法表示为（　　）

  A．7×10-9

  B．7×10-8

  C．0.7×10-9

  D．0.7×10-8
  组卷：6147引用：80难度：0.8

  解析

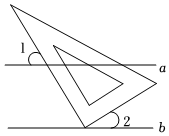• 6．如图，直角三角板的直角顶点放在直线b上，且a∥b,∠1=55°，则∠2的度数为（　　）

  A．35°

  B．45°

  C．55°

  D．25°
  组卷：1602引用：13难度：0.8

  解析

• 7．如图，线段AB与线段CD关于点P对称，若点A（3，3）、B（5，1）、D（-3，-1），则点C的坐标为（　　）

  A．（-3，-3）

  B．（-1，-3）

  C．（-4，-2）

  D．（-2，-4）
  组卷：834引用：6难度：0.5

  解析

• 8．给出下列判断，正确的是（　　）

  A．一组对边相等，另一组对边平行的四边形是平行四边形

  B．对角线相等的四边形是矩形

  C．对角线互相垂直且相等的四边形是正方形

  D．有一条对角线平分一个内角的平行四边形为菱形
  组卷：1665引用：17难度：0.6

  解析

三、解答题：（本大题共10个小题，共80分.解答应写出文字说明、证明过程或演算步骤.）

• 25．温州某学校的学生进行综合实践活动时，探究每盆植株培育株数与市场销售价格之间的关系，通过实验和市场调查发现，每盆植株在5株以内（含5株），植株的品质较高，单株售价3元，超过5株后，每盆每多种1株，单株售价降低0.3元，当每盆种植株株数超过12株后，植株品质较低，市场统一收购价单株0.8元，每盆最多可种植18株．
  （1）设每盆种植x（5≤x≤12）株，
  ①则单株售价

  元，每盆售价

  元（用含x的代数式表示）；
  ②当每盆售价为16.2元时，求x的值．
  （2）该学生实验小组共种植了40盆，每盆培育所需费用y（元）与每盆种植株数x（株）之间满足y=2+0.3x,每盆植株除培育费用外无其他支出．该小组将其中10盆赠送给学校，其余放至市场出售，全部售出后销售所得扣除培育费用后还剩余100元，求每盆的种植株数．
  组卷：563引用：5难度：0.6

  解析

• 26．【模型定义】
  如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．
  
  【探究应用】
  ①已知点M，N是线段AB的勾股分割点，若AM=2，MN=3，则BN=

  ；
  ②如图2，在△ABC中，FG是中位线，点D，E是线段BC的勾股分割点，且EC＞DE＞BD，连接AD，AE分别交FG于点M，N，求证：点M，N是线段FG的勾股分割点；
  【问题解决】
  如图3，已知点M，N是线段AB的勾股分割点，MN＞AM＞BN，四边形AMDC，四边形MNFE和四边形NBHG均是正方形，点P在边EF上，试探究S_△ACN，S_△APB，S_△MBH的数量关系．
  组卷：29引用：1难度：0.3

  解析