2022-2023学年广东省深圳市南山区桃源中学九年级（上）第一次月考数学试卷

一、选择题（每题3分，共36分）

• 1．下列四个银行标志中，既是中心对称图形，又是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1250引用：34难度：0.9

  解析

• 2．如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕点C顺时针旋转至△AB'C使得点A恰好落在AB上，则旋转角度为（　　）

  A．30°

  B．60°

  C．90°

  D．150°
  组卷：570引用：10难度：0.6

  解析

• 3．对于二次函数y=x²-2mx-3，下列结论错误的是（　　）

  A．它的图象与x轴有两个交点

  B．方程x2-2mx=3的两根之积为-3

  C．它的图象的对称轴在y轴的右侧

  D．x＜m时，y随x的增大而减小
  组卷：2133引用：12难度：0.7

  解析

• 4．已知m、n、4分别是等腰三角形（非等边三角形）三边的长，且m、n是关于x的一元二次方程x²-6x+k+2=0的两个根，则k的值等于（　　）

  A．7

  B．7或6

  C．6或-7

  D．6
  组卷：2700引用：19难度：0.6

  解析

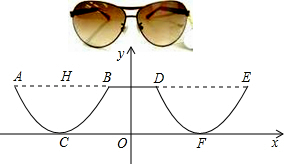• 5．为了美观，在加工太阳镜时将下半部分轮廓制作成抛物线的形状（如图所示），对应的两条抛物线关于y轴对称，AE∥x轴，AB=4cm,最低点C在x轴上，高CH=1cm,BD=2cm,则右轮廓DFE所在抛物线的解析式为（　　）

  A．y= 1 4 （x+3）2	B．y= 1 4 （x-3）2
  C．y=- 1 4 （x+3）2	D．y=- 1 4 （x-3）2
  组卷：1353引用：14难度：0.9

  解析

• 6．若（m²+n²）（1-m²-n²）+6=0，则m²+n²的值为（　　）

  A．3

  B．-2

  C．3或-2

  D．-3或2
  组卷：76引用：4难度：0.7

  解析

• 7．已知a,b是关于x的一元二次方程x²+（2m+3）x+m²=0的两个不相等的实数根，且满足

  1

  a

  +

  1

  b

  =

  -

  1

  ，则m的值是（　　）

  A．-3或1

  B．3或-1

  C．3

  D．1
  组卷：1005引用：6难度：0.6

  解析

三、解答题

• 22．如图，一次函数

  y

  =

  -

  1

  2

  x

  +

  2

  分别交y轴、x轴于A、B两点，抛物线y=-x²+bx+c过A、B两点．
  （1）求这个抛物线的解析式；
  （2）作垂直x轴的直线x=t,在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，MN有最大值？最大值是多少？
  （3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标．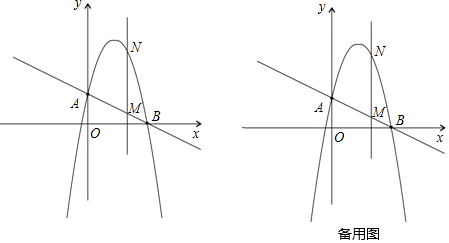
  
  组卷：2590引用：62难度：0.5

  解析

• 23．已知抛物线y=ax²+bx-4经过点A（2，0）、B（-4，0），与y轴交于点C．
  （1）求这条抛物线的解析式；
  （2）如图1，点P是第三象限内抛物线上的一个动点，当四边形ABPC的面积最大时，求点P的坐标；
  （3）如图2，线段AC的垂直平分线交x轴于点E，垂足为D，M为抛物线的顶点，在直线DE上是否存在一点G，使△CMG的周长最小？若存在，求出点G的坐标；若不存在，请说明理由．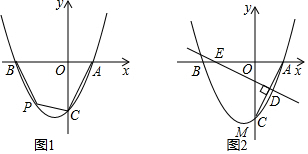
  
  组卷：3634引用：10难度：0.3

  解析