2022-2023学年山东省淄博市高青县八年级（下）期末数学试卷（五四学制）

一、选择题（本题有10小题，每小题4分，共40分，每小题只有一个选项是正确的，不选、多选、错选，均不得分）

• 1．下列各式中属于最简二次根式的是（　　）

  A． x 2 y 5

  B． 0 . 5

  C． 12

  D． x 2 + 1
  组卷：288引用：11难度：0.9

  解析

• 2．若关于x的一元二次方程kx²+2x-1=0有实数根，则k的取值范围是（　　）

  A．k＞-1

  B．k≥-1

  C．k＞-1且k≠0

  D．k≥-1且k≠0
  组卷：974引用：71难度：0.9

  解析

• 3．已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是（　　）

  A．选①②

  B．选①③

  C．选②④

  D．选②③
  组卷：1590引用：28难度：0.9

  解析

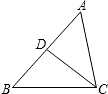• 4．如图所示，给出下列条件：①∠B=∠ACD；②∠ADC=∠ACB；③

  AC

  CD

  =

  AB

  BC

  ；④AC²=AD•AB．其中能够判定△ABC∽△ACD的个数为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：1790引用：141难度：0.9

  解析

• 5．设

  5

  =

  m

  ,

  7

  =

  n

  ，则

  0

  .

  056

  可以表示为（　　）

  A． mn 10

  B． mn 15

  C． mn 20

  D． mn 25
  组卷：1464引用：9难度：0.6

  解析

• 6．已知x=2是关于x的方程x²-（m+4）x+4m=0的一个实数根，并且这个方程的两个实数根恰好是等腰三角形ABC的两条边长，则△ABC的周长为（　　）

  A．6

  B．8

  C．10

  D．8或10
  组卷：1991引用：23难度：0.7

  解析

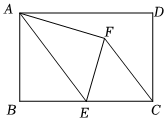• 7．如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为（　　）

  A． 18 5

  B． 12 5

  C． 16 5

  D． 9 5
  组卷：760引用：7难度：0.5

  解析

三、解答题（共8小题，共90分）

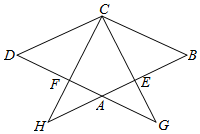• 22．已知：如图，在菱形ABCD中，点E、F分别在边AB、AD上，BE=DF，CE的延长线交DA的延长线于点G，CF的延长线交BA的延长线于点H．
  （1）求证：△BEC∽△BCH；
  （2）如果BE²=AB•AE，求证：AG=DF．
  组卷：4731引用：21难度：0.5

  解析

• 23．操作与证明：如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AF．取AF中点M，EF的中点N，连接MD、MN．
  （1）连接AE，求证：△AEF是等腰三角形；
  猜想与发现：
  （2）在（1）的条件下，请判断MD、MN的数量关系和位置关系，得出结论．
  结论1：DM、MN的数量关系是

  ；
  结论2：DM、MN的位置关系是

  ；
  拓展与探究：
  （3）如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．
  组卷：3739引用：25难度：0.5

  解析