2020-2021学年安徽省芜湖二十九中八年级（上）期中数学试卷
发布：2024/9/7 18:0:8
一、选择题（本大题共10小题，每题4分，共40分）
-
1．若△ABC满足下列某个条件，则它不是直角三角形的是（ ）
组卷：1142引用：8难度：0.6 -
2．如果三角形的两边长分别为3和5，则周长L的取值范围是（ ）
组卷：1883引用：15难度：0.7 -
3．如图，在△ABC中，AB=4，AC=3，AD平分∠BAC，则S△ABD：S△ADC为（ ）组卷：279引用：10难度：0.7 -
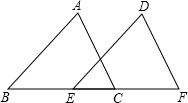4．如图，在△ABC和△DEF中，∠B=∠DEF，AB=DE，添加下列一个条件后，仍然不能证明△ABC≌△DEF，这个条件是（ ）组卷：7900引用：77难度：0.9 -
5．已知a＞0，b＜0，则点P（a+1，b-1）关于x轴对称的点一定在（ ）
组卷：13引用：1难度：0.7 -
6．如图，已知△ABC中，∠ABC=45°，F是高AD和BE的交点，CD=4，则线段DF的长度为（ ）组卷：884引用：34难度：0.9 -
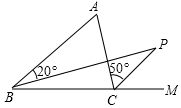7．如图，BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，如果∠ABP=20°，∠ACP=50°，则∠A+∠P=（ ）组卷：2688引用：30难度：0.6
三、解答题（本大题共8小题，共85分）
-
22．概念学习
规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．
从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．
理解概念
（1）如图1，在Rt△ABC中，∠ACB=90°，CD⊥AB，请写出图中两对“等角三角形”．
概念应用
（2）如图2，在△ABC中，CD为角平分线，∠A=40°，∠B=60°．
求证：CD为△ABC的等角分割线．
（3）在△ABC中，∠A=42°，CD是△ABC的等角分割线，直接写出∠ACB的度数．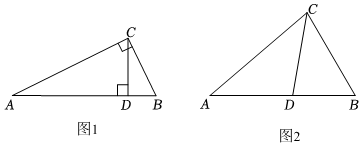
组卷：2387引用：25难度：0.1 -
23．如图1，已知A（0，a），B（b,0）且a,b满足（a-2）2+|4-b|=0．
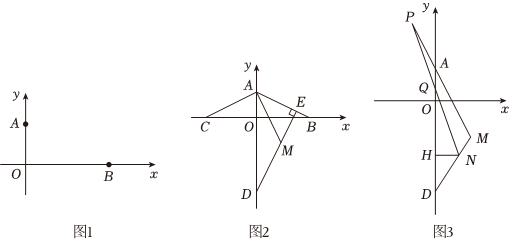
（1）求A、B两点的坐标；
（2）如图2，连接AB，若D（0，-6），DE⊥AB于点E，B、C关于y轴对称，M是线段DE上的一点，且DM=AB，连接AM，试判断线段AC与AM之间的位置和数量关系，并证明你的结论；
（3）如图3，在（2）的条件下，若N是线段DM上的一个动点，P是MA延长线上的一点，且DN=AP，连接PN交y轴于点Q，过点N作NH⊥y轴于点H，当N点在线段DM上运动时线段QH是否为定值？若是，请求出这个值；若不是，请说明理由．组卷：238引用：8难度：0.1
